MacAdam ellipse

In the study of color vision, a MacAdam ellipse is a region on a chromaticity diagram which contains all colors which are indistinguishable, to the average human eye, from the color at the center of the ellipse. The contour of the ellipse therefore represents the just-noticeable differences of chromaticity. Standard Deviation Color Matching in LED lighting uses deviations relative to MacAdam ellipses to describe color precision of a light source.[1]

MacAdam ellipses for one of MacAdam's test participants, Perley G. Nutting (observer "PGN"), plotted on the CIE 1931 xy chromaticity diagram. The ellipses are ten times their actual size, as depicted in MacAdam's paper.

History

In the study of color perception, the first question that usually comes to mind is, "What color is it?" In other words, we wish to develop a method of specifying a particular color which allows us to differentiate it from all other colors. It has been found that three quantities are needed to specify a particular color. The relative amounts of red, green and blue in a color will serve to specify that color completely. This question was first approached by a number of researchers in the 1930s, and their results were formalized in the specification of the CIE XYZ color space.

The second question we might ask, given two colors, is, "How different are these two colors?" Just as the first question was answered by developing a color space in which three numbers specified a particular color, we are now asking effectively, how far apart these two colors are. This particular question was considered by researchers dating back to Helmholtz and Schrödinger,[2] and later in industrial applications,[3] but experiments by Wright and Pitt,[4] and David MacAdam provided much-needed empirical support.[5]

Procedure

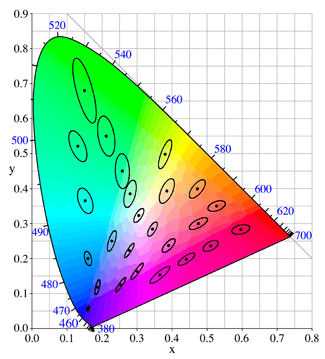
MacAdam set up an experiment in which a trained observer viewed two different colors, at a fixed luminance of about 48 cd/m2. One of the colors (the "test" color) was fixed, but the other was adjustable by the observer, and the observer was asked to adjust that color until it matched the test color. This match was, of course, not perfect, since the human eye, like any other instrument, has limited accuracy. It was found by MacAdam, however, that all of the matches made by the observer fell into an ellipse on the CIE 1931 chromaticity diagram. The measurements were made at 25 points on the chromaticity diagram, and it was found that the size and orientation of the ellipses on the diagram varied widely depending on the test color. These 25 ellipses measured by MacAdam, for a particular observer, are shown on the chromaticity diagram above.

Extension to three dimensions

A more general concept is that of "discrimination ellipsoids" in the entire three-dimensional color space, which would include the ability of an observer to discriminate between two different luminances of the same color.[6] Such measurements were carried out, among others, by Brown and MacAdam in 1949,[7] Davidson in 1951,[8] Brown in 1957,[9] and by Wyszecki and Fielder in 1971.[10] It was found that the discrimination ellipsoids yielded relatively unchanging discrimination ellipses in chromaticity space for luminances between 3 and 30 cd/m2.[7]

Effects in colour theory

MacAdam's results confirmed earlier suspicions that colour difference could be measured using a metric in a chromaticity space. A number of attempts have been made to define a color space which is not as distorted as the CIE XYZ space. The most notable of these are the CIELUV and CIELAB color spaces. Although both of these spaces are less distorted than the CIE XYZ space, they are not completely free of distortion. This means that the MacAdam ellipses become nearly (but not exactly) circular in these spaces.

gollark: If you do do this, I'd like to at least advise on a modpack.
gollark: https://www.curseforge.com/minecraft/mc-mods/realistic-terrain-generation would be nice too.
gollark: There is that mod to autogenerate a city by McJty, which would be nicer than a player-designed world.
gollark: As I said, with "no cheating"/"no being a toxic idiot" (and other obvious ones) as the rules, and no claims, and *enough players*, and a decent modpack, it could be fun.
gollark: I see.

See also

References
  1. "Talking Photometry - Colour Difference". Photometric Testing. Retrieved 26 March 2017.
  2. Kühni, Rolf G. (March 2003). "6. Historical Development of Color Space and Color Difference Formulas". Color Space and Its Divisions. New York: Wiley. doi:10.1002/0471432261.ch6. ISBN 978-0-471-32670-0.
  3. Judd, Deane B. (July 1939). "Specification of Color Tolerances at the National Bureau of Standards". The American Journal of Psychology. The American Journal of Psychology, Vol. 52, No. 3. 52 (3): 418–428. doi:10.2307/1416753. JSTOR 1416753.
  4. Wright, William David; Pitt, F.H.G. (May 1934). "Hue-discrimination in normal colour-vision". Proceedings of the Physical Society. 46 (3): 459–473. doi:10.1088/0959-5309/46/3/317.
  5. MacAdam, David Lewis (May 1942). "Visual sensitivities to color differences in daylight" (abstract). JOSA. 32 (5): 247–274. doi:10.1364/JOSA.32.000247.
  6. Günter Wyszecki and Walter Stanley Stiles, Color Science: Concepts and Methods, Quantitative Data and Formula (2nd edition), Wiley-Interscience. (July 28, 2000). ISBN 0-471-39918-3
  7. Brown, Walter R.J.; MacAdam, David L. (October 1949). "Visual sensitivities to combined chromaticity and luminance differences" (abstract). JOSA. 39 (10): 808–834. doi:10.1364/JOSA.39.000808.
  8. Davidson, Hugh R. (December 1951). "Calculation of Color Differences from Visual Sensitivity Ellipsoids" (abstract). JOSA. 41 (12): 1052–1056. doi:10.1364/JOSA.41.001052.
  9. Brown, Walter R.J. (February 1957). "Color Discrimination of Twelve Observers" (abstract). JOSA. 47 (2): 137–143. doi:10.1364/JOSA.47.000137.
  10. Wyszecki, Günter; Fielder, G. H. (September 1971). "New Color-Matching Ellipses" (abstract). JOSA. 61 (9): 1135–1152. doi:10.1364/JOSA.61.001135.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.