Locally linear graph

In graph theory, a locally linear graph is an undirected graph in which the neighborhood of every vertex is an induced matching. That is, for every vertex ${\displaystyle v}$, every neighbor of ${\displaystyle v}$ should be adjacent to exactly one other neighbor of ${\displaystyle v}$. Equivalently, every edge ${\displaystyle uv}$ of such a graph belongs to a unique triangle ${\displaystyle uvw}$.[1] Locally linear graphs have also been called locally matched graphs.[2]

The nine-vertex Paley graph is locally linear. One of its six triangles is highlighted in green.

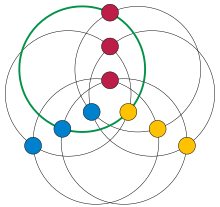
Examples of locally linear graphs include the triangular cactus graphs, the line graphs of 3-regular triangle-free graphs, and the Cartesian products of smaller locally linear graphs. Certain Kneser graphs, and certain strongly regular graphs, are also locally linear.

Some locally linear graphs have a number of edges that is near-quadratic. The question of how dense these graphs can be is one of the formulations of the Ruzsa–Szemerédi problem. The densest planar graphs that can be locally linear are also known.

Constructions and examples

The cuboctahedron, a planar locally linear graph that can be formed as the line graph of a cube or by gluing antiprisms onto the inside and outside faces of a 4-cycle

Several constructions for locally linear graphs are known.

Gluing and products

The friendship graphs, graphs formed by gluing together a collection of triangles at a single shared vertex, are locally linear. They are the only finite graphs having the stronger property that every pair of vertices (adjacent or not) share exactly one common neighbor.[3] More generally every triangular cactus graph, a graph in which all simple cycles are triangles and all pairs of simple cycles have at most one vertex in common, is locally linear.

Let ${\displaystyle G}$ and ${\displaystyle H}$ be any two locally linear graphs, select a triangle from each of them, and glue the two graphs together by identifying corresponding pairs of vertices in these triangles (this is a form of the clique-sum operation on graphs). Then the resulting graph remains locally linear.[4]

The Cartesian product of any two locally linear graphs remains locally linear, because any triangles in the product come from triangles in one or the other factors. For instance, the nine-vertex Paley graph (the graph of the 3-3 duoprism) is the Cartesian product of two triangles.[1] The Hamming graphs ${\displaystyle H(d,3)}$ are products of ${\displaystyle d}$ triangles, and again are locally linear.[5]

Expansion

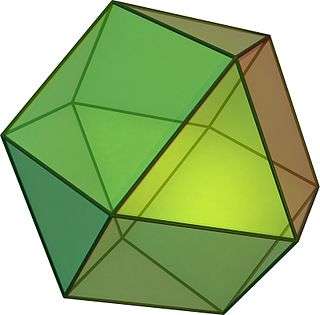
If ${\displaystyle G}$ is a 3-regular triangle-free graph, then the line graph ${\displaystyle L(G)}$ is a graph formed by expanding each edge of ${\displaystyle G}$ into a new vertex, and making two vertices adjacent in ${\displaystyle L(G)}$ when the corresponding edges of ${\displaystyle G}$ share an endpoint. These graphs are 4-regular and locally linear. Every 4-regular locally linear graph can be constructed in this way.[6] For instance, the graph of the cuboctahedron can be formed in this way as the line graph of a cube, and the nine-vertex Paley graph is the line graph of the utility graph ${\displaystyle K_{3,3}}$. The line graph of the Petersen graph, another graph of this type, has a property analogous to the cages in that it is the smallest possible graph in which the largest clique has three vertices, each vertex is in exactly two edge-disjoint cliques, and the shortest cycle with edges from distinct cliques has length five.[7]

A more complicated expansion process applies to planar graphs. Let ${\displaystyle G}$ be a planar graph embedded in the plane in such a way that every face is a quadrilateral, such as the graph of a cube. Necessarily, if ${\displaystyle G}$ has ${\displaystyle n}$ vertices, it has ${\displaystyle n-2}$ faces. Gluing a square antiprism onto each face of ${\displaystyle G}$, and then deleting the original edges of ${\displaystyle G}$, produces a new locally linear planar graph with ${\displaystyle 5(n-2)+2}$ vertices and ${\displaystyle 12(n-2)}$ edges.[4] For instance, the cuboctahedron can again be produced in this way, from the two faces (the interior and exterior) of a 4-cycle.

Algebraic constructions

A Kneser graph ${\displaystyle KG_{a,b}}$ has ${\displaystyle {\tbinom {a}{b}}}$ vertices, representing the ${\displaystyle b}$-element subsets of an ${\displaystyle a}$-element set. Two vertices are adjacent when the corresponding subsets are disjoint. When ${\displaystyle a=3b}$ the resulting graph is locally linear, because for each two disjoint ${\displaystyle b}$-element subsets there is exactly one other ${\displaystyle b}$-element subset (the complement of their union) that is disjoint from both of them. The resulting locally linear graph has ${\displaystyle {\tbinom {3b}{b}}}$ vertices and ${\displaystyle {\tfrac {1}{2}}{\tbinom {3b}{b}}{\tbinom {2b}{b}}}$ edges. For instance, for ${\displaystyle b=2}$ the Kneser graph ${\displaystyle KG_{6,2}}$ is locally linear with 15 vertices and 45 edges.[2]

Locally linear graphs can also be constructed from progression-free sets of numbers. Let ${\displaystyle p}$ be a prime number, and let ${\displaystyle A}$ be a subset of the numbers modulo ${\displaystyle p}$ such that no three members of ${\displaystyle A}$ form an arithmetic progression modulo ${\displaystyle p}$. (That is, ${\displaystyle A}$ is a Salem–Spencer set modulo ${\displaystyle p}$.) Then there exists a tripartite graph in which each side of the tripartition has ${\displaystyle p}$ vertices, there are ${\displaystyle 3|A|p}$ edges, and each edge belongs to a unique triangle. To construct this graph, number the vertices on each side of the tripartition from ${\displaystyle 0}$ to ${\displaystyle p-1}$, and construct triangles of the form ${\displaystyle (x,x+a,x+2a)}$ modulo ${\displaystyle p}$ for each ${\displaystyle x}$ in the range from ${\displaystyle 0}$ to ${\displaystyle p-1}$ and each ${\displaystyle a}$ in ${\displaystyle A}$. The graph formed from the union of these triangles has the desired property that every edge belongs to a unique triangle. For, if not, there would be a triangle ${\displaystyle (x,x+a,x+a+b)}$ where ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c=(a+b)/2}$ all belong to ${\displaystyle A}$, violating the assumption that there be no arithmetic progressions ${\displaystyle (a,c,b)}$ in ${\displaystyle A}$.[8] For example, with ${\displaystyle p=3}$ and ${\displaystyle A=\{\pm 1\}}$, the result is the nine-vertex Paley graph.

Regular and strongly regular graphs

Every locally linear graph must have even degree at each vertex, because the edges at each vertex can be paired up into triangles. The Cartesian product of two locally linear regular graphs is again locally linear and regular, with degree equal to the sum of the degrees of the factors. Therefore, there exist regular locally linear graphs of every even degree.[1] The ${\displaystyle 2r}$-regular locally linear graphs must have at least ${\displaystyle 6r-3}$ vertices, because there are this many vertices among any triangle and its neighbors alone. (No two vertices of the triangle can share a neighbor without violating local linearity.) Regular graphs with exactly this many vertices are possible only when ${\displaystyle r}$ is 1, 2, 3, or 5, and are uniquely defined for each of these four cases. The four regular graphs meeting this bound on the number of vertices are the 3-vertex 2-regular triangle ${\displaystyle K_{3}}$, the 9-vertex 4-regular Paley graph, the 15-vertex 6-regular Kneser graph ${\displaystyle KG_{6,2}}$, and the 27-vertex 10-regular complement graph of the Schläfli graph. The final 27-vertex 10-regular graph also represents the intersection graph of the 27 lines on a cubic surface.[2]

A strongly regular graph can be characterized by a quadruple of parameters ${\displaystyle (n,k,\lambda ,\mu )}$ where ${\displaystyle n}$ is the number of vertices, ${\displaystyle k}$ is the number of incident edges per vertex, ${\displaystyle \lambda }$ is the number of shared neighbors for every adjacent pair of vertices, and ${\displaystyle \mu }$ is the number of shared neighbors for every non-adjacent pair of vertices. When ${\displaystyle \lambda =1}$ the graph is locally linear. The locally linear graphs already mentioned above that are strongly regular graphs and their parameters are

• the triangle (3,2,1,0),
• the nine-vertex Paley graph (9,4,1,2),
• the Kneser graph ${\displaystyle KG_{6,2}}$ (15,6,1,3), and
• the complement of the Schläfli graph (27,10,1,5).

Other locally linear strongly regular graphs include

• the Brouwer–Haemers graph (81,20,1,6),[9]
• the Berlekamp–van Lint–Seidel graph (243,22,1,2),[10]
• the Cossidente–Penttila graph (378,52,1,8),[11] and
• the Games graph (729,112,1,20).[12]

Other potentially-valid combinations with ${\displaystyle \lambda =1}$ include (99,14,1,2) and (115,18,1,3) but it is unknown whether strongly regular graphs with those parameters exist.[13] The question of the existence of a strongly regular graph with parameters (99,14,1,2) is known as Conway's 99-graph problem, and John Horton Conway has offered a $1000 prize for its solution.[14]

There are finitely many distance-regular graphs of degree 4 or 6 that are locally linear. Beyond the strongly regular graphs of the same degrees, they also include the line graph of the Petersen graph, the Hamming graph ${\displaystyle H(3,3)}$, and the halved Foster graph.[15]

Density

The densest possible locally linear planar graphs are formed by gluing an antiprism (red vertices and black edges) into each quadrilateral face of a planar graph (blue vertices and dashed yellow edges)

Main article: Ruzsa–Szemerédi problem

One formulation of the Ruzsa–Szemerédi problem asks for the maximum number of edges in an ${\displaystyle n}$-vertex locally linear graph. As Imre Z. Ruzsa and Endre Szemerédi proved, this maximum number is ${\displaystyle o(n^{2})}$ but is ${\displaystyle \Omega (n^{2-\varepsilon })}$ for every ${\displaystyle \varepsilon >0}$. The construction of locally linear graphs from progression-free sets leads to the densest known locally linear graphs, with ${\displaystyle n^{2}/\exp O({\sqrt {\log n}})}$ edges.[8]

Among planar graphs, the maximum number of edges in a locally linear graph with ${\displaystyle n}$ vertices is ${\displaystyle {\tfrac {12}{5}}(n-2)}$. The graph of the cuboctahedron is the first in an infinite sequence of polyhedral graphs with ${\displaystyle n=5k+2}$ vertices and ${\displaystyle {\tfrac {12}{5}}(n-2)=12k}$ edges, for ${\displaystyle k=2,3,\dots }$, constructed by expanding the quadrilateral faces of ${\displaystyle K_{2,k}}$ into antiprisms. These examples show that this upper bound is tight.[4]

References

1. Fronček, Dalibor (1989), "Locally linear graphs", Mathematica Slovaca, 39 (1): 3–6, hdl:10338.dmlcz/136481, MR 1016323
2. Larrión, F.; Pizaña, M. A.; Villarroel-Flores, R. (2011), "Small locally nK₂ graphs" (PDF), Ars Combinatoria, 102: 385–391, MR 2867738
3. Erdős, Paul; Rényi, Alfréd; Sós, Vera T. (1966), "On a problem of graph theory" (PDF), Studia Sci. Math. Hungar., 1: 215–235
4. Zelinka, Bohdan (1988), "Polytopic locally linear graphs", Mathematica Slovaca, 38 (2): 99–103, hdl:10338.dmlcz/133017, MR 0945363
5. Devillers, Alice; Jin, Wei; Li, Cai Heng; Praeger, Cheryl E. (2013), "Local 2-geodesic transitivity and clique graphs", Journal of Combinatorial Theory, Series A, 120 (2): 500–508, doi:10.1016/j.jcta.2012.10.004, MR 2995054. In the notation of this reference, the family of ${\displaystyle 2r}$-regular graphs is denoted as ${\displaystyle F(r,2)}$.
6. Munaro, Andrea (2017), "On line graphs of subcubic triangle-free graphs", Discrete Mathematics, 340 (6): 1210–1226, doi:10.1016/j.disc.2017.01.006, MR 3624607
7. Fan, Cong (1996), "On generalized cages", Journal of Graph Theory, 23 (1): 21–31, doi:10.1002/(SICI)1097-0118(199609)23:1<21::AID-JGT2>3.0.CO;2-M, MR 1402135
8. Ruzsa, I. Z.; Szemerédi, E. (1978), "Triple systems with no six points carrying three triangles", Combinatorics (Proc. Fifth Hungarian Colloq., Keszthely, 1976), Vol. II, Colloq. Math. Soc. János Bolyai, 18, Amsterdam and New York: North-Holland, pp. 939–945, MR 0519318
9. Brouwer, A. E.; Haemers, W. H. (1992), "Structure and uniqueness of the (81,20,1,6) strongly regular graph", A collection of contributions in honour of Jack van Lint, Discrete Mathematics, 106/107: 77–82, doi:10.1016/0012-365X(92)90532-K, MR 1181899
10. Berlekamp, E. R.; van Lint, J. H.; Seidel, J. J. (1973), "A strongly regular graph derived from the perfect ternary Golay code", A Survey of Combinatorial Theory (Proc. Internat. Sympos., Colorado State Univ., Fort Collins, Colo., 1971), Amsterdam: North-Holland: 25–30, doi:10.1016/B978-0-7204-2262-7.50008-9, ISBN 9780720422627, MR 0364015
11. Cossidente, Antonio; Penttila, Tim (2005), "Hemisystems on the Hermitian surface", Journal of the London Mathematical Society, Second Series, 72 (3): 731–741, doi:10.1112/S0024610705006964, MR 2190334
12. Bondarenko, Andriy V.; Radchenko, Danylo V. (2013), "On a family of strongly regular graphs with ${\displaystyle \lambda =1}$", Journal of Combinatorial Theory, Series B, 103 (4): 521–531, arXiv:1201.0383, doi:10.1016/j.jctb.2013.05.005, MR 3071380
13. Makhnëv, A. A. (1988), "Strongly regular graphs with ${\displaystyle \lambda =1}$", Akademiya Nauk SSSR, 44 (5): 667–672, 702, doi:10.1007/BF01158426, MR 0980587
14. Zehavi, Sa'ar; David de Olivera, Ivo Fagundes (2017), Not Conway's 99-graph problem, arXiv:1707.08047
15. Hiraki, Akira; Nomura, Kazumasa; Suzuki, Hiroshi (2000), "Distance-regular graphs of valency 6 and ${\displaystyle a_{1}=1}$", Journal of Algebraic Combinatorics, 11 (2): 101–134, doi:10.1023/A:1008776031839, MR 1761910