Ljubljana graph

In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges.[1]

Ljubljana graph
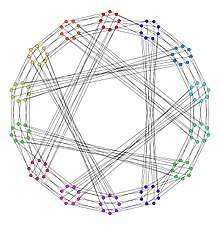The Ljubljana graph as a covering graph of the Heawood graph
Vertices112
Edges168
Radius7
Diameter8
Girth10
Automorphisms168
Chromatic number2
Chromatic index3
PropertiesCubic
Semi-symmetric
Hamiltonian
Table of graphs and parameters

It is a cubic graph with diameter 8, radius 7, chromatic number 2 and chromatic index 3. Its girth is 10 and there are exactly 168 cycles of length 10 in it. There are also 168 cycles of length 12.[2]

Construction

The Ljubljana graph is Hamiltonian and can be constructed from the LCF notation : [47, -23, -31, 39, 25, -21, -31, -41, 25, 15, 29, -41, -19, 15, -49, 33, 39, -35, -21, 17, -33, 49, 41, 31, -15, -29, 41, 31, -15, -25, 21, 31, -51, -25, 23, 9, -17, 51, 35, -29, 21, -51, -39, 33, -9, -51, 51, -47, -33, 19, 51, -21, 29, 21, -31, -39]2.

The Ljubljana graph is the Levi graph of the Ljubljana configuration, a quadrangle-free configuration with 56 lines and 56 points.[2] In this configuration, each line contains exactly 3 points, each point belongs to exactly 3 lines and any two lines intersect in at most one point.

Algebraic properties

The automorphism group of the Ljubljana graph is a group of order 168. It acts transitively on the edges the graph but not on its vertices : there are symmetries taking every edge to any other edge, but not taking every vertex to any other vertex. Therefore, the Ljubljana graph is a semi-symmetric graph, the third smallest possible cubic semi-symmetric graph after the Gray graph on 54 vertices and the Iofinova-Ivanov graph on 110 vertices.[3]

The characteristic polynomial of the Ljubljana graph is

History

The Ljubljana graph was first published in 1993 by Brouwer, Dejter and Thomassen[4] as a self-complementary subgraph of the Dejter graph. [5]

In 1972, Bouwer was already talking of a 112-vertices edge- but not vertex-transitive cubic graph found by R. M. Foster, nonetheless unpublished.[6] Conder, Malnič, Marušič, Pisanski and Potočnik rediscovered this 112-vertices graph in 2002 and named it the Ljubljana graph after the capital of Slovenia.[2] They proved that it was the unique 112-vertices edge- but not vertex-transitive cubic graph and therefore that was the graph found by Foster.

  • The Ljubljana graph is Hamiltonian and bipartite
  • The chromatic index of the Ljubljana graph is 3.
  • Alternative drawing of the Ljubljana graph.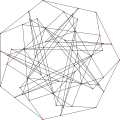
  • The Ljubljana graph is the Levi graph of this configuration.
gollark: I can *also* make anything use 32GB of RAM.
gollark: One of my friends has a bunch of servers with something like 48GB of memory each which they use *only* for bad PHP applications and Windows VMs or something.
gollark: In-memory caching of beeoids?
gollark: Why did you do that?
gollark: Suffer?

References
  1. Weisstein, Eric W. "Ljubljana Graph". MathWorld.
  2. Conder, M.; Malnič, A.; Marušič, D.; Pisanski, T.; and Potočnik, P. "The Ljubljana Graph." 2002. .
  3. Marston Conder, Aleksander Malnič, Dragan Marušič and Primž Potočnik. "A census of semisymmetric cubic graphs on up to 768 vertices." Journal of Algebraic Combinatorics: An International Journal. Volume 23, Issue 3, pages 255-294, 2006.
  4. Brouwer, A. E.; Dejter, I. J.; and Thomassen, C. "Highly Symmetric Subgraphs of Hypercubes." J. Algebraic Combinat. 2, 25-29, 1993.
  5. Klin M.; Lauri J.; Ziv-Av M. "Links between two semisymmetric graphs on 112 vertices through the lens of association schemes", Jour. Symbolic Comput., 47–10, 2012, 1175–1191.
  6. Bouwer, I. A. "On Edge But Not Vertex Transitive Regular Graphs." J. Combin. Th. Ser. B 12, 32-40, 1972.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.