Line of greatest slope

In topography, the line of greatest slope is a curve following the steepest slope. In mountain biking and skiing, the line of greatest slope is sometimes called the fall line.[1]

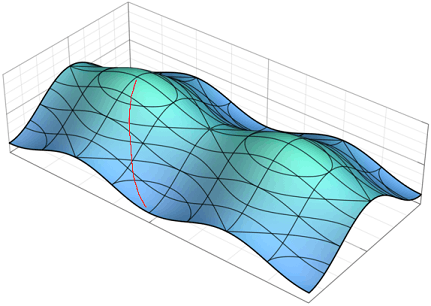
A surface showing one example (approximate) of a path of greatest slope (red path).

Definition

Mathematically, the line (or path) of greatest slope from a point is determined by the gradient of height, taken as a potential field with respect to an acceleration from the force of gravity. Lines of greatest slope are analogous to lines of force acting to accelerate an object downward at that point. These lines are orthogonal to contour lines. Discounting inertial forces and terrain roughness, a ball rolling down a slope, or water flowing down, will accelerate in the direction of greatest slope.

Applications

Mountain biking
A mountain biker riding a trail which follows the line of greatest slope, or fall line.

In mountain biking the line of greatest slope defines the fall line, which is the path a trail will follow to descend a hill or mountain with the shortest path,[1] and will also cause the rider to gain the most velocity (assuming brakes are not used, and other factors such as rolling resistance are equal).

Mountain climbing
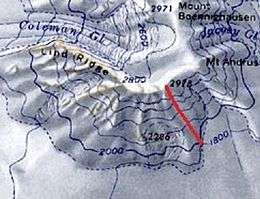
The line of greatest slope defines the path (red) a climber will take to gain the most elevation with the shortest possible path.

In mountain climbing, the line of greatest slope defines the fall line, which is the path a climber will take to gain the most elevation with the shortest possible path.

Map reading

The line of greatest slope has practical significance in map reading. On the terrain it is often far more discernible, even intuitively obvious, rather than accurately picking out the consistent height level on what is likely the undulating uneven ground along the ground represented on the contour line. But knowing that a greatest slope vector is orthogonal to the contour line, one can readily deduce the direction of the contour lines from the line of greatest slope. The extent and overall direction of the contour line to a map scale can only be found on the topographic map.

By noting the corresponding compass vector, walking along the contour one can line up a hand held compass aligning the expected direction, and eye-balling the line of contour's estimated level, move up or down along the bearing faster— to closely locate a desired point (planned point) along the hillside. Pragmatically, this can be 'good enough' for rough project landscaping, such as timber clear cutting the work site of a structure like a bridge abutment or connecting ramps. The approximation can then be refined by transit and other surveyor tools to construct on target.

gollark: <@332271551481118732> fix.
gollark: V5's compiler doesn't have this?
gollark: RPNCalcV6 with do notation WHEN?
gollark: I predicted this, yes.
gollark: I thought an RPNCalc ± operator would be neat but then realised it would need either arrays somehow or duplicated code.

See also

References
  1. https://rootsrated.com Farlow Gap – Mountain Biking: fall line (2nd paragraph) — "The trail becomes loose and rocky, and becomes fall line into a wide open rock garden..."
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.