Lexicographic product of graphs
In graph theory, the lexicographic product or (graph) composition G ∙ H of graphs G and H is a graph such that
- the vertex set of G ∙ H is the cartesian product V(G) × V(H); and
- any two vertices (u,v) and (x,y) are adjacent in G ∙ H if and only if either u is adjacent with x in G or u = x and v is adjacent with y in H.
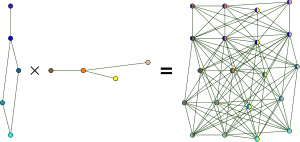
If the edge relations of the two graphs are order relations, then the edge relation of their lexicographic product is the corresponding lexicographic order.
The lexicographic product was first studied by Felix Hausdorff (1914). As Feigenbaum & Schäffer (1986) showed, the problem of recognizing whether a graph is a lexicographic product is equivalent in complexity to the graph isomorphism problem.
Properties
The lexicographic product is in general noncommutative: G ∙ H ≠ H ∙ G. However it satisfies a distributive law with respect to disjoint union: (A + B) ∙ C = A ∙ C + B ∙ C. In addition it satisfies an identity with respect to complementation: C(G ∙ H) = C(G) ∙ C(H). In particular, the lexicographic product of two self-complementary graphs is self-complementary.
The independence number of a lexicographic product may be easily calculated from that of its factors (Geller & Stahl 1975):
- α(G ∙ H) = α(G)α(H).
The clique number of a lexicographic product is as well multiplicative:
- ω(G ∙ H) = ω(G)ω(H).
The chromatic number of a lexicographic product is equal to the b-fold chromatic number of G, for b equal to the chromatic number of H:
- χ(G ∙ H) = χb(G), where b = χ(H).
The lexicographic product of two graphs is a perfect graph if and only if both factors are perfect (Ravindra & Parthasarathy 1977).
References
- Feigenbaum, J.; Schäffer, A. A. (1986), "Recognizing composite graphs is equivalent to testing graph isomorphism", SIAM Journal on Computing, 15 (2): 619–627, doi:10.1137/0215045, MR 0837609.
- Geller, D.; Stahl, S. (1975), "The chromatic number and other functions of the lexicographic product", Journal of Combinatorial Theory, Series B, 19: 87–95, doi:10.1016/0095-8956(75)90076-3, MR 0392645.
- Hausdorff, F. (1914), Grundzüge der Mengenlehre, Leipzig
- Imrich, Wilfried; Klavžar, Sandi (2000), Product Graphs: Structure and Recognition, Wiley, ISBN 0-471-37039-8
- Ravindra, G.; Parthasarathy, K. R. (1977), "Perfect product graphs", Discrete Mathematics, 20 (2): 177–186, doi:10.1016/0012-365X(77)90056-5, hdl:10338.dmlcz/102469, MR 0491304.