Self-complementary graph

A self-complementary graph is a graph which is isomorphic to its complement. The simplest non-trivial self-complementary graphs are the 4-vertex path graph and the 5-vertex cycle graph.

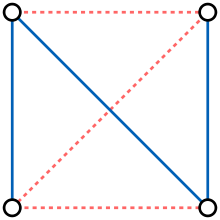
A self-complementary graph: the blue N is isomorphic to its complement, the dashed red Z.

Examples

Every Paley graph is self-complementary.[1] For example, the 3 × 3 rook's graph (the Paley graph of order nine) is self-complementary, by a symmetry that keeps the center vertex in place but exchanges the roles of the four side midpoints and four corners of the grid.[2] All strongly regular self-complementary graphs with fewer than 37 vertices are Paley graphs; however, there are strongly regular graphs on 37, 41, and 49 vertices that are not Paley graphs.[3]

The Rado graph is an infinite self-complementary graph.[4]

Properties

An n-vertex self-complementary graph has exactly half number of edges of the complete graph, i.e., n(n − 1)/4 edges, and (if there is more than one vertex) it must have diameter either 2 or 3.[1] Since n(n −1) must be divisible by 4, n must be congruent to 0 or 1 mod 4; for instance, a 6-vertex graph cannot be self-complementary.

Computational complexity

The problems of checking whether two self-complementary graphs are isomorphic and of checking whether a given graph is self-complementary are polynomial-time equivalent to the general graph isomorphism problem.[5]

gollark: why avaritia
gollark: Why?
gollark: ++remind 1h Uninvite them, maybe.
gollark: Stuff without worldgen can be added retroactively anyway.
gollark: I can't see anything obvious missing, I guess.

References
  1. Sachs, Horst (1962), "Über selbstkomplementäre Graphen", Publicationes Mathematicae Debrecen, 9: 270–288, MR 0151953.
  2. Shpectorov, S. (1998), "Complementary l1-graphs", Discrete Mathematics, 192 (1–3): 323–331, doi:10.1016/S0012-365X(98)0007X-1, MR 1656740.
  3. Rosenberg, I. G. (1982), "Regular and strongly regular selfcomplementary graphs", Theory and practice of combinatorics, North-Holland Math. Stud., 60, Amsterdam: North-Holland, pp. 223–238, MR 0806985.
  4. Cameron, Peter J. (1997), "The random graph", The mathematics of Paul Erdős, II, Algorithms Combin., 14, Berlin: Springer, pp. 333–351, arXiv:1301.7544, Bibcode:2013arXiv1301.7544C, MR 1425227. See in particular Proposition 5.
  5. Colbourn, Marlene J.; Colbourn, Charles J. (1978), "Graph isomorphism and self-complementary graphs", SIGACT News, 10 (1): 25–29, doi:10.1145/1008605.1008608.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.