Kepler–Bouwkamp constant

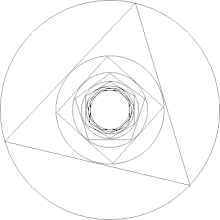
In plane geometry, the Kepler–Bouwkamp constant (or polygon inscribing constant) is obtained as a limit of the following sequence. Take a circle of radius 1. Inscribe a regular triangle in this circle. Inscribe a circle in this triangle. Inscribe a square in it. Inscribe a circle, regular pentagon, circle, regular hexagon and so forth. The radius of the limiting circle is called the Kepler–Bouwkamp constant (Finch, 2003). It is named after Johannes Kepler and Christoffel Bouwkamp, and is the inverse of the polygon circumscribing constant.

A sequence of inscribed polygons and circles

Numerical value

The decimal expansion of the Kepler–Bouwkamp constant is (sequence A085365 in the OEIS)

${\displaystyle \prod _{k=3}^{\infty }\cos \left({\frac {\pi }{k}}\right)=0.1149420448\dots .}$

The natural logarithm of the Kepler-Bouwkamp constant is given by

${\displaystyle -2\sum _{k=1}^{\infty }{\frac {2^{2k}-1}{2k}}\zeta (2k)\left(\zeta (2k)-1-{\frac {1}{2^{2k}}}\right)}$

where ${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}}$ is the Riemann zeta function.

If the product is taken over the odd primes, the constant

${\displaystyle \prod _{k=3,5,7,11,13,17,\ldots }\cos \left({\frac {\pi }{k}}\right)=0.312832\ldots }$

is obtained (sequence A131671 in the OEIS).

References

• Finch, S. R. (2003). Mathematical Constants. Cambridge University Press. MR 2003519.

Further reading

• Kitson, Adrian R. (2006). "The prime analog of the Kepler–Bouwkamp constant". arXiv:math/0608186.
• Kitson, Adrian R. (2008). "The prime analogue of the Kepler-Bouwkamp constant". The Mathematical Gazette. 92: 293. doi:10.1017/S0025557200183214.
• Doslic, Tomislav (2014). "Kepler-Bouwkamp radius of combinatorial sequences". Journal of Integer Sequence. 17: 14.11.3.

External links

• Weisstein, Eric W. "Polygon Inscribing". MathWorld.