Kalah
Kalah, also called Kalaha or Mancala, is a game in the mancala family imported in the United States by William Julius Champion, Jr. in 1940. This game is sometimes also called "Kalahari", possibly by false etymology from the Kalahari desert in Namibia.
| Kalah | |
|---|---|
| Ranks | Two |
| Sowing | Single lap |
| Region | United States, United Kingdom |
As the most popular and commercially available variant of mancala in the West, Kalah is also sometimes referred to as Warri or Awari, although those names more properly refer to the game Oware.
For most of its variations, Kalah is a solved game with a first-player win if both players play perfect games. The Pie rule can be used to balance the first-player's advantage.
Example turn
The player begins sowing from the highlighted house.
The last seed falls in the store, so the player receives an extra move.
The last seed falls in an empty house on the player's side. The player collects the highlighted seeds from both his house and the opposite house of his opponent and will move them to the store.
The game provides a Kalah board and a number of seeds or counters. The board has 6 small pits, called houses, on each side; and a big pit, called an end zone, at each end. The object of the game is to capture more seeds than one's opponent.
- At the beginning of the game, four seeds are placed in each house. This is the traditional method.
- Each player controls the six houses and their seeds on the player's side of the board. The player's score is the number of seeds in the store to their right.
- Players take turns sowing their seeds. On a turn, the player removes all seeds from one of the houses under their control. Moving counter-clockwise, the player drops one seed in each house in turn, including the player's own store but not their opponent's.
- If the last sown seed lands in an empty house owned by the player, and the opposite house contains seeds, both the last seed and the opposite seeds are captured and placed into the player's store.
- If the last sown seed lands in the player's store, the player gets an additional move. There is no limit on the number of moves a player can make in their turn.
- When one player no longer has any seeds in any of their houses, the game ends. The other player moves all remaining seeds to their store, and the player with the most seeds in their store wins.
It is possible for the game to end in a draw.
Variations
- The game may start with a number of seeds in each house different from four. A nomenclature has been developed to describe these variations: Kalah(h,s), where h designates the number of houses on each side, and s designates the number of seeds that start out in each house. In broad terms, the more seeds, the more challenging is the game. The three-, four-, five- and six-seed Kalah have been solved, with the starting player always winning with perfect play.[1][2] Thus some web sites have implemented the game with the pie rule to make it fair.
- An alternative rule has players sow in a clockwise direction, requiring more stones to be sowed in a single turn to reach the store.
- The "Empty Capture" variant: If the last sown seed lands in an empty house owned by the player, even if the opposite house is empty, the last seed is captured and placed into the player's store.
- An alternative rule does not count the remaining seeds as part of the opponent's score at the end of the game.
Computer analysis of Kalah
Mark Rawlings has written a computer program to extensively analyze both the "standard" version of Kalah and the "empty capture" version, which is the primary variant. The analysis was made possible by the creation of the largest endgame databases ever made for Kalah. They include the perfect play result of all 38,902,940,896 positions with 34 or fewer seeds. In 2015, for the first time ever, each of the initial moves for the standard version of Kalah(6,4) and Kalah(6,5) have been quantified: Kalah(6,4) is a proven win by 8 for the first player and Kalah(6,5) is a proven win by 10 for the first player. In addition, Kalah(6,6) with the standard rules has been proven to be at least a win by 4. Further analysis of Kalah(6,6) with the standard rules is ongoing.
For the "empty capture" version, Geoffrey Irving and Jeroen Donkers (2000) proved that Kalah(6,4) is a win by 10 for the first player with perfect play, and Kalah(6,5) is a win by 12 for the first player with perfect play. Anders Carstensen (2011) proved that Kalah(6,6) was a win for the first player. Mark Rawlings (2015) has extended these "empty capture" results by fully quantifying the initial moves for Kalah(6,4), Kalah(6,5), and Kalah(6,6). With searches totaling 106 days and over 55 trillion nodes, he has proven that Kalah(6,6) is a win by 2 for the first player with perfect play. This was a surprising result, given that the "4-seed" and "5-seed" variations are wins by 10 and 12, respectively. Kalah(6,6) is extremely deep and complex when compared to the 4-seed and 5-seed variations, which can now be solved in a fraction of a second and less than a minute, respectively.
The endgame databases created by Mark Rawlings were loaded into RAM during program initialization (takes 17 minutes to load). So the program could run on a computer with 32GB of RAM, the 30-seed and 33-seed databases were not loaded.
Endgame database counts: seeds position count cumulative count ------------------------------------------- 2-25 1,851,010,435 1,851,010,435 26 854,652,330 2,705,662,765 27 1,202,919,536 3,908,582,301 28 1,675,581,372 5,584,163,673 29 2,311,244,928 7,895,408,601 30 3,158,812,704 11,054,221,305 31 4,279,807,392 15,334,028,697 32 5,751,132,555 21,085,161,252 33 7,668,335,248 28,753,496,500 34 10,149,444,396 38,902,940,896 -------------------------------------------
For the following sections, bins are numbered as shown, with play in a counter-clockwise direction. South moves from bins 1 through 6 and North moves from bins 8 through 13. Bin 14 is North's store and bin 7 is South's store.
<--- North
------------------------
13 12 11 10 9 8
14 7
1 2 3 4 5 6
------------------------
South --->
Kalah(6,4)
Starting position with 4 seeds in each bin:
<--- North
------------------------
4 4 4 4 4 4
0 0
4 4 4 4 4 4
------------------------
South --->
The following tables show the results of each of the 10 possible first player moves (assumes South moves first) for both the standard rules and for the "empty capture" variant. Note that there are 10 possible first moves, since moves from bin 3 result in a "move-again." Search depth continued until the game ended.
Standard Rules: move result perfect play continuation ------------------------------------------------------- 1 lose by 14 10 13 3 9 13 12 1 13 11 5 13 2 lose by 10 10 13 5 9 13 8 4 10 13 8 5 3-1 lose by 6 10 11 2 13 1 12 1 13 9 4 12 3-2 tie 10 13 5 9 13 8 3 11 1 13 10 3-4 win by 2 10 9 13 2 1 12 3 5 8 12 13 3-5 win by 4 9 10 2 5 12 1 2 11 2 13 5 3-6 win by 8 9 8 2 12 6 5 11 6 1 6 5 4 lose by 2 10 12 2 4 13 1 5 9 13 12 13 5 lose by 8 10 9 11 2 5 10 1 8 4 12 5 6 win by 4 9 12 2 6 1 11 4 10 6 5 13 -------------------------------------------------------
"Empty Capture" Variant: move result perfect play continuation ------------------------------------------------------- 1 lose by 14 10 13 4 9 13 11 2 13 8 13 10 2 lose by 8 10 13 5 9 13 8 4 10 13 9 5 3-1 lose by 8 10 11 4 9 12 2 10 5 11 12 9 3-2 lose by 2 10 13 5 9 13 8 3 11 5 13 10 3-4 win by 2 10 9 13 2 1 12 3 5 8 12 13 3-5 win by 4 9 11 2 4 8 12 5 13 5 11 4 3-6 win by 10 9 8 4 11 6 2 6 4 9 5 13 4 lose by 2 10 12 2 5 9 8 12 9 4 10 11 5 lose by 6 10 9 11 4 8 13 5 6 4 12 6 6 win by 4 9 12 2 6 1 11 4 10 6 5 13 -------------------------------------------------------
Kalah(6,5)
Starting position with 5 seeds in each bin:
<--- North
------------------------
5 5 5 5 5 5
0 0
5 5 5 5 5 5
------------------------
South --->
The following tables show the results of each of the 10 possible first player moves (assumes South moves first) for both the standard rules and for the "empty capture" variant. Note that there are 10 possible first moves, since moves from bin 2 result in a "move-again." Search depth continued until the game ended.
Standard Rules: move result perfect play continuation ------------------------------------------------------- 1 lose by 10 9 11 4 8 13 2 9 6 3 11 13 2-1 lose by 4 9 10 2 12 1 11 3 12 8 11 1 2-3 win by 10 10 1 6 9 5 13 6 2 8 4 13 2-4 win by 10 8 11 1 6 9 2 13 11 4 12 6 2-5 win by 8 8 10 1 6 9 5 13 12 2 13 11 2-6 tie 8 11 1 6 3 11 6 5 12 6 8 3 win by 2 9 8 12 1 4 11 2 12 10 4 3 4 win by 2 8 11 1 5 12 3 10 5 2 11 6 5 win by 2 8 12 1 4 9 2 12 4 9 3 11 6 tie 8 12 1 6 4 10 6 2 11 4 3 -------------------------------------------------------
"Empty Capture" Variant: move result perfect play continuation ------------------------------------------------------- 1 lose by 10 9 12 6 8 12 11 2 8 6 5 12 2-1 lose by 6 9 10 2 12 4 8 9 3 10 11 3 2-3 win by 12 8 10 1 6 10 5 13 9 6 4 11 2-4 win by 8 8 9 1 6 11 4 13 10 4 13 9 2-5 win by 8 8 10 1 6 9 5 13 12 3 13 6 2-6 lose by 2 8 11 1 6 5 9 6 3 11 12 5 3 win by 2 9 8 12 1 4 11 2 10 4 5 10 4 tie 8 11 1 5 12 3 9 5 2 11 3 5 tie 8 10 1 4 12 5 11 2 9 4 13 6 tie 8 12 1 6 4 9 6 2 12 6 5 -------------------------------------------------------
Kalah(6,6)
Starting position with 6 seeds in each bin:
<--- North
------------------------
6 6 6 6 6 6
0 0
6 6 6 6 6 6
------------------------
South --->
The following tables show the results of each of the 10 possible first player moves (assumes South moves first) for the "empty capture" variant and the current status of the results for the standard variation. Note that there are 10 possible first moves, since moves from bin 1 result in a "move-again." Search depth for the "empty capture" variant continued until the game ended.
"Standard" Variant: (Results are still being computed by Mark Rawlings.) move result ------------------------------------------------------- 1-2 proven win, by at least 2 1-3 proven win, by at least 4 1-4 1-5 1-6 proven loss, by at least 2 2 trending towards a win 3 4 5 6 proven loss, by at least 2 ------------------------------------------------------- The remaining moves (1-4, 1-5, 3, 4, and 5) are probable ties based on very deep searches, however, the result has not yet been proven.
"Empty Capture" Variant: move result perfect play continuation ------------------------------------------------------- 1-2 win by 2 10 3 12 4 8 6 10 11 6 3... 1-3 win by 2 11 1 8 2 10 6 8 3 11 5... 1-4 tie 10 3 12 5 10 3 9 1 12 3... 1-5 tie 9 4 8 3 10 2 10 4 1 9... 1-6 tie 10 4 9 6 3 11 6 8 2 10... 2 win by 2 12 4 10 1 12 8 1 11 3 9... 3 tie 10 5 12 4 11 1 12 8 4 3... 4 tie 10 3 11 1 9 5 11 2 10 8... 5 tie 10 3 11 4 12 2 11 4 10 5... 6 loss by 2 10 3 8 6 4 13 1 10 13 8... -------------------------------------------------------
A breakdown of the 55+ trillion nodes searched to solve the "empty capture" variant of Kalah(6,6):
move time (sec) nodes searched ---------------------------------------- 1-2 305,791 2,214,209,715,560 1-3 403,744 2,872,262,354,066 1-4 401,349 2,335,350,353,288 1-5 317,795 1,886,991,523,192 1-6 392,923 2,313,607,567,702 2 1,692,886 9,910,945,999,186 3 1,296,141 7,398,319,653,760 4 1,411,091 9,623,816,064,478 5 1,607,514 9,318,824,643,697 6 1,354,845 7,824,794,014,305 ---------------------------------------- total 9,184,079 55,699,121,889,234
Mathematical analysis
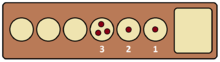
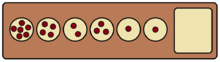
As mentioned above, if the last seed sown by a player lands in that player's store, the player gets an extra move. A clever player can take advantage of this rule to chain together many, many extra turns. Certain configurations of a row of the board can in this way be cleared in a single turn, that is, the player can capture all stones on their row, as depicted on the right. The longest possible such chain on a standard Kalah board of six pits lasts for seventeen moves. On a general n-pit board, the patterns of seeds which can be cleared in a single turn in this way have been the object of mathematical study.[3] One can prove that, for all n, there exists one and only one pattern clearable in exactly n moves, or equivalently, one and only one clearable pattern consisting of exactly n seeds.
These patterns require arbitrarily long rows of pits and n increases. For example, it can be seen on the right that the unique 5-seed pattern requires only 3 pits, but the 17-seed pattern requires 6 pits. The relationship between the required number of pits and the number of seeds can be described in the following way. Let s(n) denote the minimum number of seeds which requires n pits to clear. Then where the symbol denotes asymptotic equivalence, that is, , or equivalently, .[3]
Terminology and Tactics
Basic aspects of the game (by Chris Bandy):
- Stash: a house with seeds in it, esp. a large amount, making it desirable for the opponent to capture.
- Strike: a move that results in a capture of an opponent's stash.
- Target: the empty house that you land in, in order to capture an opponent's stash.
- Attack: a move that puts you in a position where you could strike on your next turn.
- Block: a move that removes the threat created by an opponent's attack.
- Sequence: a series of moves in a single turn (achieved by continuously landing in your own store).
- Double: attacking an enemy stash with two of your own houses simultaneously.
- Counter: responding to an attack with your own attack (instead of blocking).
There are two types of strikes:
- Short-strike: emptying a house with 1-5 seeds.
- Long-strike: emptying a house with 8-13 seeds. Long strikes are harder to spot, and give you 2 more seeds on average (one from the seed you deposited in your store, and one from the seed you deposited in the stash you are striking).
There are three types of blocks:
- Dodge: empty the attacked house.
- Cover: empty a house in order to fill the opponent's target hole.
- Neutralize: capture the attacking house (usually, this is only available if the opponent has made a blunder).
There are five levels of stashes:
- Short-strikers: 1-5 seeds
- Sequencers: 6 seeds
- Useless: 7 seeds
- Long-strikers: 8-13 seeds
- Wrappers: 14+ seeds
Since even novice players can spot open attacks (there are only six places to check), more advanced players organize hidden strikes. A hidden strike is when you use a sequence to open up an attack and execute the strike in the same turn. For example (using the diagram above), you've got 1 seed in 5 and 6, and your opponent has a stash in 8. You can open the attack by emptying 6, and then short-strike with 5 in the same turn. This sort of attack is harder to spot than an open attack.
An even more advanced form of hidden strikes are concealed strikes. A concealed strike is when you increase one of your own houses in a sequence to open up an attack. For example, you've got 2 seeds in 5, and 7 seeds in 6, and your opponent has a stash in 13. You can open the attack by emptying 5, thus increasing house 6 to 8 seeds. Then you can long-strike with 6, taking the 13 stash.
References
- Solving Kalah by Geoffrey Irving, Jeroen Donkers and Jos Uiterwijk.
- Solving (6,6)-Kalaha by Anders Carstensen.
- Broline, Duane M.; Loeb, Daniel E. (1995-02-08). "The combinatorics of Mancala-type games: Ayo, Tchoukaitlon, and 1/π". arXiv:math/9502225.