Fourth, fifth, and sixth derivatives of position

In physics, the fourth, fifth and sixth derivatives of position are defined as derivatives of the position vector with respect to time – with the first, second, and third derivatives being velocity, acceleration, and jerk, respectively. However, given that these higher-order derivatives appear more rarely than lower-order ones,[1] their names are not as standardized.

Time-derivatives of position

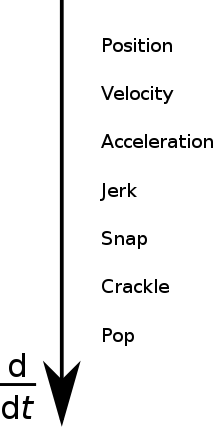
The fourth derivative is often referred to as snap or jounce. Because of the name "snap" for the fourth derivative, proposed names for the fifth and sixth derivatives include crackle and pop respectively[2] — inspired by the advertising mascots Snap, Crackle, and Pop[3] — which are used, though "sometimes somewhat facetiously".[3]

Fourth derivative (snap/jounce)

Snap,[4] or jounce, is the fourth derivative of the position vector with respect to time, or the rate of change of the jerk with respect to time.[3] Equivalently, it is the second derivative of acceleration or the third derivative of velocity, and is defined by any of the following equivalent expressions:

${\displaystyle {\vec {s}}={\frac {d\,{\vec {\jmath }}}{dt}}={\frac {d^{2}{\vec {a}}}{dt^{2}}}={\frac {d^{3}{\vec {v}}}{dt^{3}}}={\frac {d^{4}{\vec {r}}}{dt^{4}}}.}$

The following equations are used for constant snap:

${\displaystyle {\vec {\jmath }}={\vec {\jmath }}_{0}+{\vec {s}}t,}$

${\displaystyle {\vec {a}}={\vec {a}}_{0}+{\vec {\jmath }}_{0}t+{\frac {1}{2}}{\vec {s}}t^{2},}$

${\displaystyle {\vec {v}}={\vec {v}}_{0}+{\vec {a}}_{0}t+{\frac {1}{2}}{\vec {\jmath }}_{0}t^{2}+{\frac {1}{6}}{\vec {s}}t^{3},}$

${\displaystyle {\vec {r}}={\vec {r}}_{0}+{\vec {v}}_{0}t+{\frac {1}{2}}{\vec {a}}_{0}t^{2}+{\frac {1}{6}}{\vec {\jmath }}_{0}t^{3}+{\frac {1}{24}}{\vec {s}}t^{4},}$

where

${\displaystyle {\vec {s}}}$ is constant snap,

${\displaystyle {\vec {\jmath }}_{0}}$ is initial jerk,

${\displaystyle {\vec {\jmath }}}$ is final jerk,

${\displaystyle {\vec {a}}_{0}}$ is initial acceleration,

${\displaystyle {\vec {a}}}$ is final acceleration,

${\displaystyle {\vec {v}}_{0}}$ is initial velocity,

${\displaystyle {\vec {v}}}$ is final velocity,

${\displaystyle {\vec {r}}_{0}}$ is initial position,

${\displaystyle {\vec {r}}}$ is final position,

${\displaystyle t}$ is time between initial and final states.

The notation ${\displaystyle {\vec {s}}}$ (used by Visser[3]) is not to be confused with the displacement vector commonly denoted similarly.

The dimensions of snap are distance per fourth power of time. In SI units, this is "metres per second to the fourth", m/s⁴, m⋅s⁻⁴, or 100 gal per second squared in CGS units.

Fifth derivative (crackle)

Crackle[2] is the fifth derivative of the position vector with respect to time, with the first, second, third, and fourth derivatives being velocity, acceleration, jerk, and snap, respectively; crackle is thus the rate of change of the snap with respect to time.[2][3] Crackle is defined by any of the following equivalent expressions:

${\displaystyle {\vec {c}}={\frac {d{\vec {s}}}{dt}}={\frac {d^{2}{\vec {\jmath }}}{dt^{2}}}={\frac {d^{3}{\vec {a}}}{dt^{3}}}={\frac {d^{4}{\vec {v}}}{dt^{4}}}={\frac {d^{5}{\vec {r}}}{dt^{5}}}}$

The following equations are used for constant crackle:

${\displaystyle {\vec {s}}={\vec {s}}_{0}+{\vec {c}}\,t}$

${\displaystyle {\vec {\jmath }}={\vec {\jmath }}_{0}+{\vec {s}}_{0}\,t+{\frac {1}{2}}{\vec {c}}\,t^{2}}$

${\displaystyle {\vec {a}}={\vec {a}}_{0}+{\vec {\jmath }}_{0}\,t+{\frac {1}{2}}{\vec {s}}_{0}\,t^{2}+{\frac {1}{6}}{\vec {c}}\,t^{3}}$

${\displaystyle {\vec {v}}={\vec {v}}_{0}+{\vec {a}}_{0}\,t+{\frac {1}{2}}{\vec {\jmath }}_{0}\,t^{2}+{\frac {1}{6}}{\vec {s}}_{0}\,t^{3}+{\frac {1}{24}}{\vec {c}}\,t^{4}}$

${\displaystyle {\vec {r}}={\vec {r}}_{0}+{\vec {v}}_{0}\,t+{\frac {1}{2}}{\vec {a}}_{0}\,t^{2}+{\frac {1}{6}}{\vec {\jmath }}_{0}\,t^{3}+{\frac {1}{24}}{\vec {s}}_{0}\,t^{4}+{\frac {1}{120}}{\vec {c}}\,t^{5}}$

where

${\displaystyle {\vec {c}}}$ : constant crackle,

${\displaystyle {\vec {s}}_{0}}$ : initial snap,

${\displaystyle {\vec {s}}}$ : final snap,

${\displaystyle {\vec {\jmath }}_{0}}$ : initial jerk,

${\displaystyle {\vec {\jmath }}}$ : final jerk,

${\displaystyle {\vec {a}}_{0}}$ : initial acceleration,

${\displaystyle {\vec {a}}}$ : final acceleration,

${\displaystyle {\vec {v}}_{0}}$ : initial velocity,

${\displaystyle {\vec {v}}}$ : final velocity,

${\displaystyle {\vec {r}}_{0}}$ : initial position,

${\displaystyle {\vec {r}}}$ : final position,

${\displaystyle t}$ : time between initial and final states.

The dimensions of crackle are LT⁻⁵. In SI units, this is m/s⁵, and in CGS units, 100 gal per cubed second.

Sixth derivative (pop/pounce)

Pop[2] (occasionally known as Pounce) is the sixth derivative of the position vector with respect to time, with the first, second, third, fourth, and fifth derivatives being velocity, acceleration, jerk, snap, and crackle, respectively; pop is thus the rate of change of the crackle with respect to time.[2][3] Pop is defined by any of the following equivalent expressions:

${\displaystyle {\vec {p}}={\frac {d{\vec {c}}}{dt}}={\frac {d^{2}{\vec {s}}}{dt^{2}}}={\frac {d^{3}{\vec {\jmath }}}{dt^{3}}}={\frac {d^{4}{\vec {a}}}{dt^{4}}}={\frac {d^{5}{\vec {v}}}{dt^{5}}}={\frac {d^{6}{\vec {r}}}{dt^{6}}}}$

The following equations are used for constant pop:

${\displaystyle {\vec {c}}={\vec {c}}_{0}+{\vec {p}}\,t}$

${\displaystyle {\vec {s}}={\vec {s}}_{0}+{\vec {c}}_{0}\,t+{\frac {1}{2}}{\vec {p}}\,t^{2}}$

${\displaystyle {\vec {\jmath }}={\vec {\jmath }}_{0}+{\vec {s}}_{0}\,t+{\frac {1}{2}}{\vec {c}}_{0}\,t^{2}+{\frac {1}{6}}{\vec {p}}\,t^{3}}$

${\displaystyle {\vec {a}}={\vec {a}}_{0}+{\vec {\jmath }}_{0}\,t+{\frac {1}{2}}{\vec {s}}_{0}\,t^{2}+{\frac {1}{6}}{\vec {c}}_{0}\,t^{3}+{\frac {1}{24}}{\vec {p}}\,t^{4}}$

${\displaystyle {\vec {v}}={\vec {v}}_{0}+{\vec {a}}_{0}\,t+{\frac {1}{2}}{\vec {\jmath }}_{0}\,t^{2}+{\frac {1}{6}}{\vec {s}}_{0}\,t^{3}+{\frac {1}{24}}{\vec {c}}_{0}\,t^{4}+{\frac {1}{120}}{\vec {p}}\,t^{5}}$

${\displaystyle {\vec {r}}={\vec {r}}_{0}+{\vec {v}}_{0}\,t+{\frac {1}{2}}{\vec {a}}_{0}\,t^{2}+{\frac {1}{6}}{\vec {\jmath }}_{0}\,t^{3}+{\frac {1}{24}}{\vec {s}}_{0}\,t^{4}+{\frac {1}{120}}{\vec {c}}_{0}\,t^{5}+{\frac {1}{720}}{\vec {p}}\,t^{6}}$

where

${\displaystyle {\vec {p}}}$ : constant pop,

${\displaystyle {\vec {c}}_{0}}$ : initial crackle,

${\displaystyle {\vec {c}}}$ : final crackle,

${\displaystyle {\vec {s}}_{0}}$ : initial snap,

${\displaystyle {\vec {s}}}$ : final snap,

${\displaystyle {\vec {\jmath }}_{0}}$ : initial jerk,

${\displaystyle {\vec {\jmath }}}$ : final jerk,

${\displaystyle {\vec {a}}_{0}}$ : initial acceleration,

${\displaystyle {\vec {a}}}$ : final acceleration,

${\displaystyle {\vec {v}}_{0}}$ : initial velocity,

${\displaystyle {\vec {v}}}$ : final velocity,

${\displaystyle {\vec {r}}_{0}}$ : initial position,

${\displaystyle {\vec {r}}}$ : final position,

${\displaystyle t}$ : time between initial and final states.

The dimensions of pop are LT⁻⁶. In SI units, this is m/s⁶, and in CGS units, 100 gal per quartic second.

References

4. Mellinger, Daniel; Kumar, Vijay (2011). "Minimum snap trajectory generation and control for quadrotors". 2011 IEEE International Conference on Robotics and Automation. pp. 2520–2525. doi:10.1109/ICRA.2011.5980409. ISBN 978-1-61284-386-5.

External links

• Cosmography: cosmology without the Einstein equations, Matt Visser, School of Mathematics, Statistics and Computer Science, Victoria University of Wellington, 2004.