Jacket matrix

In mathematics, a jacket matrix is a square symmetric matrix ${\displaystyle A=(a_{ij})}$ of order n if its entries are non-zero and real, complex, or from a finite field, and

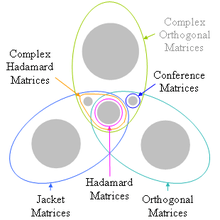
Hierarchy of matrix types

${\displaystyle \ AB=BA=I_{n}}$

where I_n is the identity matrix, and

${\displaystyle \ B={1 \over n}(a_{ij}^{-1})^{T}.}$

where T denotes the transpose of the matrix.

In other words, the inverse of a jacket matrix is determined its element-wise or block-wise inverse. The definition above may also be expressed as:

${\displaystyle \forall u,v\in \{1,2,\dots ,n\}:~a_{iu},a_{iv}\neq 0,~~~~\sum _{i=1}^{n}a_{iu}^{-1}\,a_{iv}={\begin{cases}n,&u=v\\0,&u\neq v\end{cases}}}$

The jacket matrix is a generalization of the Hadamard matrix,also it is a Diagonal block-wise inverse matrix.

Motivation

n	.... -2, -1, 0 1, 2,.....	logarithm
2^n	....${\displaystyle \ {1 \over 4},{1 \over 2},}$ 1, 2, 4,.....	Series

As shown in Table, i.e. in series, n=2 case, Forward: ${\displaystyle 2^{2}=4}$, Inverse : ${\displaystyle (2^{2})^{-1}={1 \over 4}}$, then, ${\displaystyle 4*{1 \over 4}=1}$.

Therefore, exist an element-wise inverse.

Example 1.

${\displaystyle A=\left[{\begin{array}{rrrr}1&1&1&1\\1&-2&2&-1\\1&2&-2&-1\\1&-1&-1&1\\\end{array}}\right],}$:${\displaystyle B={1 \over 4}\left[{\begin{array}{rrrr}1&1&1&1\\[6pt]1&-{1 \over 2}&{1 \over 2}&-1\\[6pt]1&{1 \over 2}&-{1 \over 2}&-1\\[6pt]1&-1&-1&1\\[6pt]\end{array}}\right].}$

or more general

${\displaystyle A=\left[{\begin{array}{rrrr}a&b&b&a\\b&-c&c&-b\\b&c&-c&-b\\a&-b&-b&a\end{array}}\right],}$:${\displaystyle B={1 \over 4}\left[{\begin{array}{rrrr}{1 \over a}&{1 \over b}&{1 \over b}&{1 \over a}\\[6pt]{1 \over b}&-{1 \over c}&{1 \over c}&-{1 \over b}\\[6pt]{1 \over b}&{1 \over c}&-{1 \over c}&-{1 \over b}\\[6pt]{1 \over a}&-{1 \over b}&-{1 \over b}&{1 \over a}\end{array}}\right],}$

Example 2.

For m x m matrices, ${\displaystyle \mathbf {A_{j}} ,}$

${\displaystyle \mathbf {A_{j}} =diag(A_{1},A_{2},..A_{n})}$ denotes an mn x mn block diagonal Jacket matrix.

${\displaystyle J_{4}=\left[{\begin{array}{rrrr}I_{2}&0&0&0\\0&cos\theta &-sin\theta &0\\0&sin\theta &cos\theta &0\\0&0&0&I_{2}\end{array}}\right],}$ ${\displaystyle \ J_{4}^{T}J_{4}=J_{4}J_{4}^{T}=I_{4}.}$

Example 3.

Euler's Formula:

${\displaystyle e^{i\pi }+1=0}$, ${\displaystyle e^{i\pi }=\cos {\pi }+i\sin {\pi }=-1}$ and ${\displaystyle e^{-i\pi }=\cos {\pi }-i\sin {\pi }=-1}$.

Therefore,

${\displaystyle e^{i\pi }e^{-i\pi }=(-1)({\frac {1}{-1}})=1}$.

Also,

${\displaystyle y=e^{x}}$

${\displaystyle {\frac {dy}{dx}}=e^{x}}$,${\displaystyle {\frac {dy}{dx}}{\frac {dx}{dy}}=e^{x}{\frac {1}{e^{x}}}=1}$.

Finally,

A·B=B·A=I

References

• Moon Ho Lee, "The Center Weighted Hadamard Transform", IEEE Transactions on Circuits Syst. Vol. 36, No. 9, PP. 1247–1249, Sept.1989.
• K.J. Horadam, Hadamard Matrices and Their Applications, Princeton University Press, UK, Chapter 4.5.1: The jacket matrix construction, PP. 85–91, 2007.
• Moon Ho Lee, Jacket Matrices: Constructions and Its Applications for Fast Cooperative Wireless Signal Processing, LAP LAMBERT Publishing, Germany,Nov. 2012.

External links

• Technical report: Linear-fractional Function, Elliptic Curves, and Parameterized Jacket Matrices
• Jacket Matrix and Its Fast Algorithms for Cooperative Wireless Signal Processing
• Jacket Matrices: Constructions and Its Applications for Fast Cooperative Wireless Signal Processing