Illumination problem

The illumination problem was posed by Ernst Gabor Straus around 1955. One form of it goes as follows. The boundary of a region in the plane acts as a mirror. A light source is put at any point inside the curve. Will every point be illuminated? In 1958 Roger Penrose solved the problem by inventing a region of which some part is left dark if the lamp is put in a certain other part. The reader should now look at his example, which can be seen free of charge, at the bottom of web page https://books.google.com/books?id=FTHZUDzW54cC&pg=PA1597 We do not reproduce the figure here, to avoid copyright issues. However, since the presentation is sketchy, we explain it in more detail. The upper part of the curve is an ellipse cut in half by its major axis. The lower part is a smooth curve under the axis except at the foci where it is tangent to the major axis. It is symmetric about the minor axis. A ray coming from one focus is reflected by an ellipse to the other focus. For later use, we call this the focal reflection property of the ellipse. Consider a ray of light coming out of the pocket. Let V be the point where it hits the ellipse. It is between the rays from V to the foci and hence its reflection will also be between those two rays and will go back into the middle pocket. Hence a light source in the middle pocket will leave the side pockets dark. Since light paths are reversible, a light source in the side pockets leaves the middle pocket dark.

 Penrose merely mentions that if one rotates the curve about its  axis of symmetry, one gets a smooth 3-dimensional region which is not illuminable from points in the middle pocket or the side groove. The insight that enabled him to conclude this was that if we rotate an ellipse about its minor axis, the ellipsoid has the following focal reflection property:

Let f be the circle described by the foci. The reflection of a ray coming from a point of f intersects f.

  To see this we need that  an oblique circular cone is also a straight elliptical cone.  This is known from analytic geometry but one can derive it without formulas just from the symmetry of the cone, as follows.
  Let  f  be the circular basis of the cone. Think of it as horizontal. Let  V  be the vertex of the cone. Let  'V'  be the vertical plane through  V  and the center of the basis circle  f.  Let  b  be the bisector of the angle formed at the vertex  V  by the two generators of the cone in the vertical plane 'V'.  Let   'P'   be a plane perpendicular to  the angle bisector  b  and not containing the vertex  V.  The intersection of  the plane  'P'  with the cone is an ellipse  e.  The symmetry about the vertical plane 'V' implies that the two points of  e  in  'V'  are the ends of an axis of  e because an ellipse is symmetric only about its major and minor axes.  The angle bisector  b  bisects this axis and is perpendicular to it. Hence the cone is a straight cone with basis  e  and axis  b.
  Now we can derive Penrose's 3-dimensional focus to focus property. Let  V  be any point on the ellipsoid. We want to prove that every ray coming to  V   from a point of the circle of foci  f  is reflected to another point of  f.  The set of rays from V  to  f  form an oblique circular cone  'C'  with vertex  V.  But  'C'  is also a straight elliptical cone, with axis perpendicular to the ellipsoid, hence it is invariant under a 180-degree rotation around its axis. This rotation changes each ray into its reflection, hence the reflection of each ray crosses the circle  f.
  We can derive that a ray  r  coming out of the central pocket is reflected back into the central pocket from the 3-dimensional focus to focus property just as in the plane case. Let  V   be the point where  r  hits the dome.  The plane formed by  r  and the normal to the surface at  V  will contain two generators of the cone. The ray  r  is between them and so will be its reflection, which will therefore go back into the pocket. Hence a source of light in the central pocket will leave the groove unlit, and vice versa.
  To construct a plane region not illuminable from any of its points, take two disjoint Penrose curves. Cut open the cental pockets of both and connect the two boundary curves so that we get a single closed curve. Now we have a curve with two half ellipses. We can think of the curve in two ways: the first half ellipse, with the rest of the curve constituting its central pocket, or the second half-ellipse, and the rest of the curve constituting its central pocket. A light source at any point will be in the central pocket of at least one of the elliptical parts and will not illuminate the side pockets of that part.  3-dimensional regions not illuminable from any of their points can be constructed in the same way.
  We observe that the "3-dimensional" non-illuminable regions given below are 2-dimensional examples made into straight cylinders, with plane mirrors at the top and bottom. One can not get a smooth surface this way.
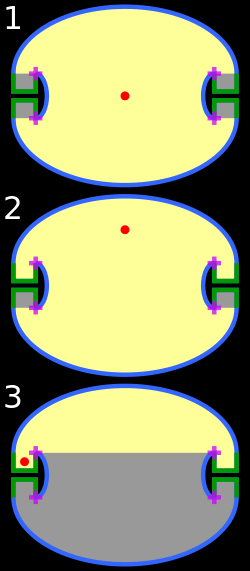
Roger Penrose's solution of the illumination problem using elliptical arcs (blue) and straight line segments (green), with 3 positions of the single light source (red spot). The purple crosses are the foci of the larger arcs. Lit and unlit regions are shown in yellow and grey, respectively.

Illumination problems are a class of mathematical problems that study the illumination of rooms with mirrored walls by point light sources.

The original formulation was attributed to Ernst Straus in the 1950s and has been resolved.[1] Straus asked if a room with mirrored walls can always be illuminated by a single point light source, allowing for repeated reflection of light off the mirrored walls. Alternatively, the question can be stated as asking that if a billiard table can be constructed in any required shape, is there a shape possible such that there is a point where it is impossible to pot the billiard ball in a pocket at another point, assuming the ball is point-like and continues infinitely rather than stopping due to friction.

The original problem was first solved in 1958 by Roger Penrose using ellipses to form the Penrose unilluminable room.[1] He showed there exists a room with curved walls that must always have dark regions if lit only by a single point source. This problem was also solved for polygonal rooms by George Tokarsky in 1995 for 2 and 3 dimensions, which showed there exists an unilluminable polygonal 26-sided room with a "dark spot" which is not illuminated from another point in the room, even allowing for repeated reflections.[2] These were rare cases, when a finite number of dark points (rather than regions) are unilluminable only from a fixed position of the point source. In 1997, two different 24-sided rooms with the same properties were put forward by G. Tokarsky and D. Castro separately.[3][4]

Solutions to the illumination problem by George W Tokarsky (26 sides) and D Castro (24 sides).

In 1995, Tokarsky found the first polygonal unilluminable room which had 4 sides and two fixed boundary points.[5] In 2016, Lelièvre, Monteil and Weiss showed that a light source in a polygonal room whose angles (in degrees) are all rational numbers will illuminate the entire polygon, with the possible exception of a finite number of points.[6]

References
  1. Weisstein, Eric W. "Illumination Problem". Wolfram Research. Retrieved 19 December 2010.
  2. Tokarsky, George (December 1995). "Polygonal Rooms Not Illuminable from Every Point". American Mathematical Monthly. University of Alberta, Edmonton, Alberta, Canada: Mathematical Association of America. 102 (10): 867–879. doi:10.2307/2975263. JSTOR 2975263.
  3. Castro, David (January–February 1997). "Corrections" (PDF). Quantum Magazine. Washington DC: Springer-Verlag. 7 (3): 42.
  4. Tokarsky, G.W. (February 1997). "Feedback, Mathematical Recreations". Scientific American. New York, N.Y.: Scientific American, Inc. 276 (2): 98. JSTOR 24993618.
  5. Tokarsky, G. (March 1995). "An Impossible Pool Shot?". SIAM Review. Philadelphia, PA: Society for Industrial and Applied Mathematics. 37 (1): 107–109. doi:10.1137/1037016.
  6. Lelièvre, Samuel; Monteil, Thierry; Weiss, Barak (4 July 2016). "Everything is illuminated". Geometry & Topology. 20 (3): 1737–1762. arXiv:1407.2975. doi:10.2140/gt.2016.20.1737.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.