Himmelblau's function
In mathematical optimization, Himmelblau's function is a multi-modal function, used to test the performance of optimization algorithms. The function is defined by:
Himmelblau's function
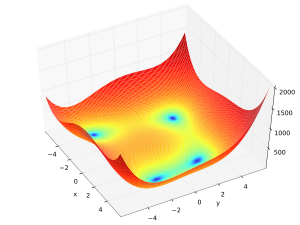
In 3D
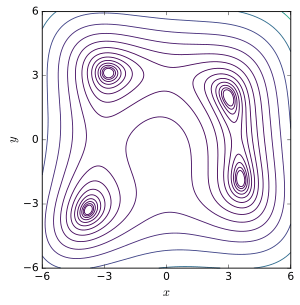
Log-spaced level curve plot
It has one local maximum at and where , and four identical local minima:
The locations of all the minima can be found analytically. However, because they are roots of cubic polynomials, when written in terms of radicals, the expressions are somewhat complicated.
The function is named after David Mautner Himmelblau (1924–2011), who introduced it.[1]
See also
References
- Himmelblau, D. (1972). Applied Nonlinear Programming. McGraw-Hill. ISBN 0-07-028921-2.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.