Heawood number

In mathematics, the Heawood number of a surface is a certain upper bound for the maximal number of colors needed to color any graph embedded in the surface.

In 1890 Heawood proved for all surfaces except the sphere that no more than

${\displaystyle H(S)=\left\lfloor {\frac {7+{\sqrt {49-24e(S)}}}{2}}\right\rfloor }$

colors are needed to color any graph embedded in a surface of Euler characteristic ${\displaystyle e(S)}$.[1] The case of the sphere is the four-color conjecture which was settled by Kenneth Appel and Wolfgang Haken in 1976.[2] [3] The number ${\displaystyle H(S)}$ became known as Heawood number in 1976.

Franklin proved that the chromatic number of a graph embedded in the Klein bottle can be as large as ${\displaystyle 6}$, but never exceeds ${\displaystyle 6}$.[4] Later it was proved in the works of Gerhard Ringel and J. W. T. Youngs that the complete graph of ${\displaystyle H(S)}$ vertices can be embedded in the surface ${\displaystyle S}$ unless ${\displaystyle S}$ is the Klein bottle.[5] This established that Heawood's bound could not be improved.

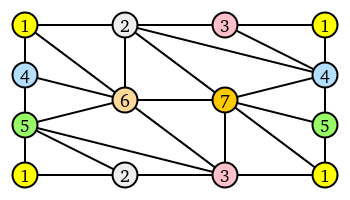
For example, the complete graph on ${\displaystyle 7}$ vertices can be embedded in the torus as follows:

Notes

• Bollobás, Béla, Graph Theory: An Introductory Course, volume 63 of GTM, Springer-Verlag, 1979. Zbl 0411.05032.
• Saaty, Thomas L. and Kainen, Paul C.; The Four-Color Problem: Assaults and Conquest, Dover, 1986. Zbl 0463.05041.

This article incorporates material from Heawood number on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

References

1. Heawood, P. J. (1890), "Map colouring theorems", Quarterly J. Math. Oxford Ser., 24: 322–339
2. Appel, Kenneth; Haken, Wolfgang (1977), "Every Planar Map is Four Colorable. I. Discharging", Illinois Journal of Mathematics, 21 (3): 429–490, MR 0543792
3. Appel, Kenneth; Haken, Wolfgang; Koch, John (1977), "Every Planar Map is Four Colorable. II. Reducibility", Illinois Journal of Mathematics, 21 (3): 491–567, doi:10.1215/ijm/1256049012, MR 0543793
4. Franklin, P. (1934), "A Six Color Problem.", Journal of Mathematics and Physics, 13 (1–4): 363–379, doi:10.1002/sapm1934131363
5. Ringel, Gerhard; Youngs, J. W. T. (1968), "Solution of the Heawood Map-Coloring Problem", Proceedings of the National Academy of Sciences, 60 (2): 438–445, doi:10.1073/pnas.60.2.438, ISSN 0027-8424, PMC 225066, PMID 16591648