Hall violator
In graph theory, a Hall violator is a set of vertices in a graph, that violate the condition to Hall's marriage theorem.[1]
Formally, given a bipartite graph G = (X + Y, E), a Hall-violator in X is a subset W of X, for which |NG(W)| < |W|, where NG(W) is the set of neighbors of W in G.
If W is a Hall violator, then there is no matching that saturates all vertices of W. Therefore, there is also no matching that saturates X. Hall's marriage theorem says that the opposite is also true: if there is no Hall violator, then there exists a matching that saturates X.
Algorithms
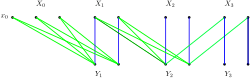
Finding a Hall violator
A Hall violator can be found by an efficient algorithm. The algorithm below uses the following terms:
- An M-alternating path, for some matching M, is a path in which the first edge is not an edge of M, the second edge is of M, the third is not of M, etc.
- A vertex z is M-reachable from some vertex x, if there is an M-alternating path from x to z.
As an example, consider the figure at the right, where the vertical (blue) edges denote the matching M. The vertex sets Y1, X1,Y2, X2, are M-reachable from x0 (or any other vertex of X0), but Y3 and X3 are not M-reachable from x0.
The algorithm for finding a Hall violator proceeds as follows.
- Find a maximum matching M (it can be found with the Hopcroft–Karp algorithm).
- If all vertices of X are matched, then return "There is no Hall violator".
- Otherwise, let x0 be an unmatched vertex.
- Let W be the set of all vertices of X that are M-reachable from x0 (it can be found using Breadth-first search; in the figure, W contains x0 and X1 and X2).
- Return W.
This W is indeed a Hall-violator because of the following facts:
- All vertices of NG(W) are matched by M. Suppose by contradiction that some vertex y in NG(W) is unmatched by M. Let x be its neighbor in W. The path from x0 to x to y is an M-augmenting path - it is M-alternating and it starts and ends with unmatched vertices, so by "inverting" it we can increase M, contradicting its maximality.
- W contains all the matches of NG(W) by M. This is because all these matches are M-reachable from x0.
- W contains another vertex - x0 - that is unmatched by M by definition.
- Hence, |W| = |NG(W)| + 1 > |NG(W)|, so W indeed satisfies the definition of a Hall violator.
Finding a minimal Hall violator
A minimal Hall violator is a Hall violator such that each of its subsets is not a Hall violator.
The above algorithm, in fact, finds a minimal Hall violator. This is because, if any vertex is removed from W, then the remaining vertices can be perfectly matched to the vertices of NG(W) (either by edges of M, or by edges of the M-alternating path from x0).[2]
Note: the above algorithm does not necessarily find a minimum-cardinality Hall violator. For example, in the above figure, it returns a Hall violator of size 5, while X0 is a Hall violator of size 3.
Finding a Hall violator or an augmenting path
The following algorithm[3][4] takes as input an arbitrary matching M in a graph, and a vertex x0 in X that is not saturated by M.
It returns as output, either a Hall violator that contains x0, or a path that can be used to augment M.
- Set k = 0, Wk := {x0}, Zk := {}.
- Assert:
- Wk = {x0,...,xk} where the xi are distinct vertices of X;
- Zk = {y1,...,yk} where the yi are distinct vertices of Y;
- For all i ≥ 1, yi is matched to xi by M.
- For all i ≥ 1, yi is connected to some xj<i by an edge not in M.
- If NG(Wk) ⊆ Zk, then Wk is a Hall violator, since |Wk| = k+1 > k = |Zk| ≥ |NG(Wk)|. Return the Hall-violator Wk.
- Otherwise, let yk+1 be a vertex in NG(Wk) \ Zk. Consider the following two cases:
- Case 1: yk+1 is matched by M.
- Since x0 is unmatched, and every xi in Wk is matched to yi in Zk, the partner of this yk+1 must be some vertex of X that is not in Wk. Denote it by xk+1.
- Let Wk+1 := Wk U {xk+1} and Zk+1 := Zk U {yk+1} and k := k + 1.
- Go back to step 2.
- Case 2: yk+1 is unmatched by M.
- Since yk+1 is in NG(Wk), it is connected to some xi (for i < k + 1) by an edge not in M. xi is connected to yi by an edge in M. yi is connected to some xj (for j < i) by an edge not in M, and so on. Following these connections must eventually lead to x0, which is unmatched. Hence we have an M-augmenting path. Return the M-augmenting path.
At each iteration, Wk and Zk grow by one vertex. Hence, the algorithm must finish after at most |X| iterations.
The procedure can be used iteratively: start with M being an empty matching, call the procedure again and again, until either a Hall violator is found, or the matching M saturates all vertices of X. This provides a constructive proof to Hall's theorem.
External links
- "Finding a subset in bipartite graph violating Hall's condition". Computer science stack exchange. 2014-09-15. Retrieved 2019-09-08.
References
- Lenchner, Jonathan (2020-01-19). "On a Generalization of the Marriage Problem". arXiv:1907.05870v3. Cite journal requires
|journal=(help) - Gan, Jiarui; Suksompong, Warut; Voudouris, Alexandros A. (2019-09-01). "Envy-freeness in house allocation problems". Mathematical Social Sciences. 101: 104–106. arXiv:1905.00468. doi:10.1016/j.mathsocsci.2019.07.005. ISSN 0165-4896.
- Mordecai J. Golin (2006). "Bipartite Matching & the Hungarian Method" (PDF).
- Segal-Halevi, Erel; Aigner-Horev, Elad (2019-01-28). "Envy-free Matchings in Bipartite Graphs and their Applications to Fair Division". arXiv:1901.09527v2. Cite journal requires
|journal=(help)