Grain boundary strengthening

Grain-boundary strengthening (or Hall–Petch strengthening) is a method of strengthening materials by changing their average crystallite (grain) size. It is based on the observation that grain boundaries are insurmountable borders for dislocations and that the number of dislocations within a grain have an effect on how stress builds up in the adjacent grain, which will eventually activate dislocation sources and thus enabling deformation in the neighbouring grain, too. So, by changing grain size one can influence the number of dislocations piled up at the grain boundary and yield strength. For example, heat treatment after plastic deformation and changing the rate of solidification are ways to alter grain size.[1]

Figure 1: Hall–Petch strengthening is limited by the size of dislocations. Once the grain size reaches about 10 nanometres (3.9×10⁻⁷ in), grain boundaries start to slide.

Theory

In grain-boundary strengthening, the grain boundaries act as pinning points impeding further dislocation propagation. Since the lattice structure of adjacent grains differs in orientation, it requires more energy for a dislocation to change directions and move into the adjacent grain. The grain boundary is also much more disordered than inside the grain, which also prevents the dislocations from moving in a continuous slip plane. Impeding this dislocation movement will hinder the onset of plasticity and hence increase the yield strength of the material.

Under an applied stress, existing dislocations and dislocations generated by Frank–Read sources will move through a crystalline lattice until encountering a grain boundary, where the large atomic mismatch between different grains creates a repulsive stress field to oppose continued dislocation motion. As more dislocations propagate to this boundary, dislocation 'pile up' occurs as a cluster of dislocations are unable to move past the boundary. As dislocations generate repulsive stress fields, each successive dislocation will apply a repulsive force to the dislocation incident with the grain boundary. These repulsive forces act as a driving force to reduce the energetic barrier for diffusion across the boundary, such that additional pile up causes dislocation diffusion across the grain boundary, allowing further deformation in the material. Decreasing grain size decreases the amount of possible pile up at the boundary, increasing the amount of applied stress necessary to move a dislocation across a grain boundary. The higher the applied stress needed to move the dislocation, the higher the yield strength. Thus, there is then an inverse relationship between grain size and yield strength, as demonstrated by the Hall–Petch equation. However, when there is a large direction change in the orientation of the two adjacent grains, the dislocation may not necessarily move from one grain to the other but instead create a new source of dislocation in the adjacent grain. The theory remains the same that more grain boundaries create more opposition to dislocation movement and in turn strengthens the material.

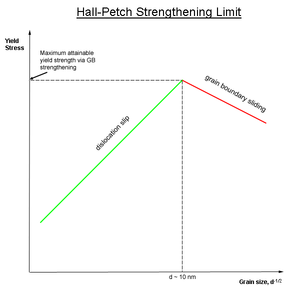
Obviously, there is a limit to this mode of strengthening, as infinitely strong materials do not exist. Grain sizes can range from about 100 μm (0.0039 in) (large grains) to 1 μm (3.9×10⁻⁵ in) (small grains). Lower than this, the size of dislocations begins to approach the size of the grains. At a grain size of about 10 nm (3.9×10⁻⁷ in),[2] only one or two dislocations can fit inside a grain (see Figure 1 above). This scheme prohibits dislocation pile-up and instead results in grain boundary diffusion. The lattice resolves the applied stress by grain boundary sliding, resulting in a decrease in the material's yield strength.

To understand the mechanism of grain boundary strengthening one must understand the nature of dislocation-dislocation interactions. Dislocations create a stress field around them given by:

${\displaystyle \sigma \propto {\frac {Gb}{r}},}$

where G is the material's shear modulus, b is the Burgers vector, and r is the distance from the dislocation. If the dislocations are in the right alignment with respect to each other, the local stress fields they create will repel each other. This helps dislocation movement along grains and across grain boundaries. Hence, the more dislocations are present in a grain, the greater the stress field felt by a dislocation near a grain boundary:

${\displaystyle \tau _{\text{felt}}=\tau _{\text{applied}}+n_{\text{dislocation}}\tau _{\text{dislocation}}\,}$

This is a schematic roughly illustrating the concept of dislocation pile-up and how it affects the strength of the material. A material with larger grain size is able to have more dislocations pile up, leading to a bigger driving force for dislocations to move from one grain to another. Thus you will have to apply less force to move a dislocation from a larger than from a smaller grain, leading materials with smaller grains to exhibit higher yield stress.

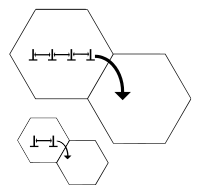
Subgrain strengthening

A subgrain is a part of the grain that is only slightly disoriented from other parts of the grain.[3] Current research is being done to see the effect of subgrain strengthening in materials. Depending on the processing of the material, subgrains can form within the grains of the material. For example, when Fe-based material is ball-milled for long periods of time (e.g. 100+ hours), subgrains of 60–90 nm are formed. It has been shown that the higher the density of the subgrains, the higher the yield stress of the material due to the increased subgrain boundary. The strength of the metal was found to vary reciprocally with the size of the subgrain, which is analogous to the Hall–Petch equation. The subgrain boundary strengthening also has a breakdown point of around a subgrain size of 0.1 µm, which is the size where any subgrains smaller than that size would decrease yield strength.[4]

Hall–Petch relationship

Hall–Petch constants[5]

Material	σ0 [MPa]	k [MPa m^1/2]
Copper	25	0.12
Titanium	80	0.40
Mild steel	70	0.74
Ni3Al	300	1.70

There is an inverse relationship between delta yield strength and grain size to some power, x.

${\displaystyle \Delta \tau \propto {k \over d^{x}}}$

where d is the strengthening coefficient and both k and x are material specific. The smaller the grain size, the smaller the repulsion stress felt by a grain boundary dislocation and the higher the applied stress needed to propagate dislocations through the material.

The relation between yield stress and grain size is described mathematically by the Hall–Petch equation:[6]

${\displaystyle \sigma _{\text{y}}=\sigma _{0}+{k_{\text{y}} \over {\sqrt {d}}}}$

where σ_y is the yield stress, σ₀ is a materials constant for the starting stress for dislocation movement (or the resistance of the lattice to dislocation motion), k_y is the strengthening coefficient (a constant specific to each material), and d is the average grain diameter. It is important to note that the H-P relationship is an empirical fit to experimental data, and that the notion that a pileup length of half the grain diameter causes a critical stress for transmission to or generation in an adjacent grain has not been verified by actual observation in the microstructure.

Theoretically, a material could be made infinitely strong if the grains are made infinitely small. This is impossible though, because the lower limit of grain size is a single unit cell of the material. Even then, if the grains of a material are the size of a single unit cell, then the material is in fact amorphous, not crystalline, since there is no long range order, and dislocations can not be defined in an amorphous material. It has been observed experimentally that the microstructure with the highest yield strength is a grain size of about 10 nm (3.9×10⁻⁷ in), because grains smaller than this undergo another yielding mechanism, grain boundary sliding.[2] Producing engineering materials with this ideal grain size is difficult because only thin films can be reliably produced with grains of this size.

History

In the early 1950s two groundbreaking series of papers were written independently on the relationship between grain boundaries and strength.

In 1951, while at the University of Sheffield, E. O. Hall wrote three papers which appeared in volume 64 of the Proceedings of the Physical Society. In his third paper, Hall[7] showed that the length of slip bands or crack lengths correspond to grain sizes and thus a relationship could be established between the two. Hall concentrated on the yielding properties of mild steels.

Based on his experimental work carried out in 1946–1949, N. J. Petch of the University of Leeds, England published a paper in 1953 independent from Hall's. Petch's paper[8] concentrated more on brittle fracture. By measuring the variation in cleavage strength with respect to ferritic grain size at very low temperatures, Petch found a relationship exact to that of Hall's. Thus this important relationship is named after both Hall and Petch.

Reverse or inverse Hall–Petch relation

The Hall–Petch relation predicts that as the grain size decreases the yield strength increases. The Hall–Petch relation was experimentally found to be an effective model for materials with grain sizes ranging from 1 millimeter to 1 micrometer. Consequently, it was believed that if average grain size could be decreased even further to the nanometer length scale the yield strength would increase as well. However, experiments on many nanocrystalline materials demonstrated that if the grains reached a small enough size, the critical grain size which is typically around 10 nm (3.9×10⁻⁷ in), the yield strength would either remain constant or decrease with decreasing grains size.[9][10] This phenomenon has been termed the reverse or inverse Hall–Petch relation. A number of different mechanisms have been proposed for this relation. As suggested by Carlton et al., they fall into four categories: (1) dislocation-based, (2) diffusion-based, (3) grain-boundary shearing-based, (4) two-phase-based.[11]

There have been several works done to investigate the mechanism behind the inverse Hall-Petch relationship on numerous materials. In Han’s work [12], a series of molecular dynamics simulations were done to investigate the effect of grain size on the mechanical properties of nanocrystalline graphene under uniaxial tensile loading, with random shapes and random orientations of graphene rings. The simulation was run at grain sizes of nm and at room temperature. It was found that in the grain size of range 3.1 nm to 40 nm, inverse Hall-Petch relationship was observed. This is because when the grain size decreases at nm scale, there is an increase in the density of grain boundary junctions which serves as a source of crack growth or weak bonding. However, it was also observed that at grain size below 3.1nm, a pseudo Hall-Petch relationship was observed, which results an increase in strength. This is due to a decrease in stress concentration of grain boundary junctions and also due to the stress distribution of 5-7 defects along the grain boundary where the compressive and tensile stress are produced by the pentagon and heptagon rings, etc. Chen at al. [13] have done research on the inverse Hall-Petch relations of high-entropy CoNiFeAlxCu1-x alloys. In the work, polycrystalline models of FCC structured CoNiFeAl0.3Cu0.7 with grain sizes ranging from 7.2nm to 18.8nm were constructed to perform uniaxial compression using molecular dynamic simulations. All compression simulations were done after setting the periodic boundary conditions across the three orthogonal directions. It was found that when the grain size is below 12.1nm the inverse Hall-Petch relation was observed. This is because as the grain size decreases partial dislocations become less prominent and so as deformation twinning. Instead, it was observed that there is a change in the grain orientation and migration of grain boundaries and thus cause the growth and shrinkage of neighboring grains. These are the mechanisms for inverse Hall-Petch relations. Sheinerman et al.[14] also studied inverse Hall-Petch relation for nanocrystalline ceramics. It was found that the critical grain size for the transition from direct Hall-Petch to inverse Hall-Petch fundamentally depends on the activation energy of grain boundary sliding. This is because in direct Hall-Petch the dominant deformation mechanism is intragrain dislocation motion while in inverse Hall-Petch the dominant mechanism is grain boundary sliding. It was concluded that by plotting both the volume fraction of grain boundary sliding and volume fraction of intragrain dislocation motion as a function of grain size, the critical grain size could be found where the two curves cross.

Other explanations that have been proposed to rationalize the apparent softening of metals with nanosized grains include poor sample quality and the suppression of dislocation pileups.[15]

The pileup of dislocations at grain boundaries is a hallmark mechanism of the Hall–Petch relationship. Once grain sizes drop below the equilibrium distance between dislocations, though, this relationship should no longer be valid. Nevertheless, it is not entirely clear what exactly the dependency of yield stress should be on grain sizes below this point.

Grain refinement

Grain refinement, also known as inoculation,[16] is the set of techniques used to implement grain boundary strengthening in metallurgy. The specific techniques and corresponding mechanisms will vary based on what materials are being considered.

One method for controlling grain size in aluminum alloys is by introducing particles to serve as nucleants, such as Al–5%Ti. Grains will grow via heterogeneous nucleation; that is, for a given degree of undercooling beneath the melting temperature, aluminum particles in the melt will nucleate on the surface of the added particles. Grains will grow in the form of dendrites growing radially away from the surface of the nucleant. Solute particles can then be added (called grain refiners) which limit the growth of dendrites, leading to grain refinement.[17] Al-Ti-B alloys are the most common grain refiner for Al alloys;[18] however, novel refiners such as Al₃Sc have been suggested.

One common technique is to induce a very small fraction of the melt to solidify at a much higher temperature than the rest; this will generate seed crystals that act as a template when the rest of the material falls to its (lower) melting temperature and begins to solidify. Since a huge number of minuscule seed crystals are present, a nearly equal number of crystallites result, and the size of any one grain is limited.

Typical inoculants for various casting alloys[16]

Metal	Inoculant
Cast iron	FeSi, SiCa, graphite
Mg alloys	Zr, C
Cu alloys	Fe, Co, Zr
Al–Si alloys	P, Ti, B, Sc
Pb alloys	As, Te
Zn alloys	Ti
Ti alloys	Al–Ti intermetallics

See also

• Strengthening mechanisms of materials

References

1. W.D. Callister. Fundamentals of Materials Science and Engineering, 2nd ed. Wiley & Sons. pp. 252.
2. Schuh, Christopher; Nieh, T.G. (2003), "Hardness and Abrasion Resistance of Nanocrystalline Nickel Alloys Near the Hall–Petch Breakdown Regime", Mater. Res. Soc. Symp. Proc., 740, doi:10.1557/proc-740-i1.8.
3. "Answers - the Most Trusted Place for Answering Life's Questions".
4. Lesuer, D.R; Syn, C.K; Sherby, O.D (2007), "Nano-subgrain strengthening in ball-milled iron", Materials Science and Engineering: A, 463 (1–2): 54–60, doi:10.1016/j.msea.2006.07.161
5. Smith & Hashemi 2006, p. 243.
6. Smith & Hashemi 2006, p. 242.
7. Hall, E.O. (1951). "The Deformation and Ageing of Mild Steel: III Discussion of Results". Proc. Phys. Soc. Lond. 64 (9): 747–753. Bibcode:1951PPSB...64..747H. doi:10.1088/0370-1301/64/9/303.
8. Petch, N.J. (1953). "The Cleavage Strength of Polycrystals". J. Iron Steel Inst. London. 173: 25–28.
9. Conrad, H; Narayan, J (2000). "On the grain size softening in nanocrystalline materials". Scripta Mater. 42 (11): 1025–30. doi:10.1016/s1359-6462(00)00320-1.
10. Park, H; Rudd, R; Cavallo, R; Barton, N; Arsenlis, A; Belof, J; Blobaum, K; El-dasher, B; Florando, J; Huntington, C; Maddox, B; May, M; Plechaty, C; Prisbrey, S; Remington, B; Wallace, R; Wehrenberg, C; Wilson, M; Comley, A; Giraldez, E; Nikroo, A; Farrell, M; Randall, G; Gray, G (2015). "Grain-Size-Independent Plastic Flow at Ultrahigh Pressures and Strain Rates". Phys. Rev. Lett. 114 (6): 065502. Bibcode:2015PhRvL.114f5502P. doi:10.1103/PhysRevLett.114.065502. PMID 25723227.
11. Carlton, C; Ferreira, P. J. (2007). "What is Behind the Inverse Hall–Petch Behavior in Nanocrystalline Materials?". Mater. Res. Soc. Symp. Proc. 976.
12. Han, Jihoon. "The transition from an inverse pseudo Hall-Petch to a pseudo Hall-Petch behavior in nanocrystalline graphene." Carbon 161 (2020): 542-549
13. Chen, Shuai, et al. "Hall-Petch and inverse Hall-Petch relations in high-entropy CoNiFeAlxCu1-x alloys." Materials Science and Engineering: A 773 (2020): 138873
14. Sheinerman, Alexander G., Ricardo HR Castro, and Mikhail Yu Gutkin. "A model for direct and inverse Hall-Petch relation for nanocrystalline ceramics." Materials Letters 260 (2020): 126886
15. Schiotz, J.; Di Tolla, F.D.; Jacobsen, K.W. (1998). "Softening of nanocrystalline metals at very small grains". Nature. 391 (6667): 561. doi:10.1038/35328.
16. Stefanescu, Doru Michael (2002), Science and engineering of casting solidification, Springer, p. 265, ISBN 978-0-306-46750-9.
17. K.T. Kashyap and T. Chandrashekar, "Effects and mechanisms of grain refinement in aluminum alloys," Bulletin of Materials Science, vol 24, August 2001
18. Fan, Z.; Wang, Y.; Zhang, Y.; Qin, T.; Zhou, X.R.; Thompson, G.E.; Pennycook, T.; Hashimoto, T. (2015). "Grain refining mechanism in the Al/Al–Ti–B system". Acta Materialia. 84: 292–304. doi:10.1016/j.actamat.2014.10.055.

Bibliography

• Smith, William F.; Hashemi, Javad (2006), Foundations of Materials Science and Engineering (4th ed.), McGraw-Hill, ISBN 978-0-07-295358-9.

External links

• Grain boundary strengthening in alumina by rare earth impurities
• Mechanism of grain boundary strengthening of steels
• An open source Matlab toolbox for analysis of slip transfer through grain boundaries