Graham–Rothschild theorem
In mathematics, the Graham–Rothschild theorem is a theorem that applies Ramsey theory to combinatorics on words and combinatorial cubes. It is named after Ronald Graham and Bruce Lee Rothschild, who published its proof in 1971.[1] Through the work of Graham, Rothschild, and Klaus Leeb in 1972, it became part of the foundations of structural Ramsey theory.[2] A special case of the Graham–Rothschild theorem motivates the definition of Graham's number, a number that was popularized by Martin Gardner in Scientific American[3] and listed in the Guinness Book of World Records as the largest number ever appearing in a mathematical proof.[4]
Background
The theorem involves sets of strings, all having the same length , over a finite alphabet, together with a group acting on the alphabet. A combinatorial cube is a subset of strings determined by constraining some positions of the string to contain a fixed letter of the alphabet, and by constraining other pairs of positions to be equal to each other or to be related to each other by the group action. This determination can be specified more formally by means of a labeled parameter word, a string with wildcard characters in the positions that are not constrained to contain a fixed letter and with additional labels describing which wildcard characters must be equal or related by the group action. The dimension of the combinatorial cube is the number of free choices that can be made for these wildcard characters. A combinatorial cube of dimension one is called a combinatorial line.[4]
For instance, in the game of tic-tac-toe, the nine cells of a tic-tac-toe board can be specified by strings of length two over the three-symbol alphabet {1,2,3} (the Cartesian coordinates of the cells), and the winning lines of three cells form combinatorial lines. Horizontal lines are obtained by fixing the -coordinate (the second position of the length-two string) and letting the -coordinate be chosen freely, and vertical lines are obtained by fixing the -coordinate and letting the -coordinate be chosen freely. The two diagonal lines of the tic-tac-toe board can be specified by a parameter word with two wildcard characters that are either constrained to be equal (for the main diagonal) or constrained to be related by a group action that swaps the 1 and 3 characters (for the antidiagonal).[5]
The set of all combinatorial cubes of dimension , for strings of length over an alphabet with group action , is denoted . A subcube of a combinatorial cube is another combinatorial cube of smaller dimension that forms a subset of the set of strings in the larger combinatorial cube. The subcubes of a combinatorial cube can also be described by a natural composition action on parameter words, obtained by substituting the symbols of one parameter word for the wildcards of another.[4]
Statement
With the notation above, the Graham–Rothschild theorem takes as parameters an alphabet , group action , finite number of colors , and two dimensions of combinatorial cubes and with . It states that, for every combination of , , , , and , there exists a string length such that, if each combinatorial cube in is assigned one of colors, then there exists a combinatorial cube in all of whose -dimensional subcubes are assigned the same color.[5]
An infinitary version of the Graham–Rothschild theorem is also known.[6]
Applications
The special case of the Graham–Rothschild theorem with , , and the trivial group action is the Hales–Jewett theorem, stating that if all long-enough strings over a given alphabet are colored, then there exists a monochromatic combinatorial line.[5]
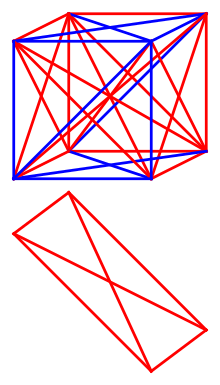
Graham's number is a bound for the Graham–Rothschild theorem with , , , , and a nontrivial group action. For these parameters, the set of strings of length over a binary alphabet describes the vertices of an -dimensional hypercube, every two of which form a combinatorial line. The set of all combinatorial lines can be described as the edges of a complete graph on the vertices. The theorem states that, for a high-enough dimension , whenever this set of edges of the complete graph is assigned two colors, there exists a monochromatic combinatorial plane: a set of four hypercube vertices that belong to a common geometric plane and have all six edges assigned the same color. Graham's number is an upper bound for this number , calculated using repeated exponentiation; it is believed to be significantly larger than the smallest for which the statement of the Graham–Rothschild theorem is true.[4]
References
- Graham, R. L.; Rothschild, B. L. (1971), "Ramsey's theorem for -parameter sets", Transactions of the American Mathematical Society, 159: 257–292, doi:10.2307/1996010, MR 0284352
- Graham, R. L.; Leeb, K.; Rothschild, B. L. (1972), "Ramsey's theorem for a class of categories", Proceedings of the National Academy of Sciences of the United States of America, 69: 119–120, doi:10.1073/pnas.69.1.119, MR 0306009; full version in Advances in Mathematics 8: 417–433, 1972, doi:10.1016/0001-8708(72)90005-9
- Gardner, Martin (November 1977), "In which joining sets of points by lines leads into diverse (and diverting) paths", Mathematical Games, Scientific American, 237 (5): 18–28, doi:10.1038/scientificamerican1177-18; revised and reprinted in The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems (2001)
- Prömel, Hans Jürgen (2002), "Large numbers, Knuth's arrow notation, and Ramsey theory", Synthese, 133 (1–2): 87–105, doi:10.1023/A:1020879709125, JSTOR 20117296, MR 1950045
- Prömel, Hans Jürgen (2013), Ramsey Theory for Discrete Structures, Springer International Publishing, pp. 41–51, doi:10.1007/978-3-319-01315-2; see in particular chapter 3 "Definitions and basic examples" (pp. 33–39, doi:10.1007/978-3-319-01315-2_3) for the definitions of parameter words and combinatorial cubes, chapter 4 "Hales–Jewett's Theorem" (pp. 41–51, doi:10.1007/978-3-319-01315-2_4) for the tic-tac-toe example, and chapter 5 "Graham–Rothschild’s Theorem" (pp. 53–59, doi:10.1007/978-3-319-01315-2_5) for the Graham–Rothschild theorem itself
- Carlson, Timothy J.; Hindman, Neil; Strauss, Dona (2006), "An infinitary extension of the Graham–Rothschild parameter sets theorem", Transactions of the American Mathematical Society, 358 (7): 3239–3262, doi:10.1090/S0002-9947-06-03899-2, MR 2216266