Gent (hyperelastic model)

The Gent hyperelastic material model [1] is a phenomenological model of rubber elasticity that is based on the concept of limiting chain extensibility. In this model, the strain energy density function is designed such that it has a singularity when the first invariant of the left Cauchy-Green deformation tensor reaches a limiting value ${\displaystyle I_{m}}$.

The strain energy density function for the Gent model is [1]

${\displaystyle W=-{\cfrac {\mu J_{m}}{2}}\ln \left(1-{\cfrac {I_{1}-3}{J_{m}}}\right)}$

where ${\displaystyle \mu }$ is the shear modulus and ${\displaystyle J_{m}=I_{m}-3}$.

In the limit where ${\displaystyle I_{m}\rightarrow \infty }$, the Gent model reduces to the Neo-Hookean solid model. This can be seen by expressing the Gent model in the form

${\displaystyle W=-{\cfrac {\mu }{2x}}\ln \left[1-(I_{1}-3)x\right]~;~~x:={\cfrac {1}{J_{m}}}}$

A Taylor series expansion of ${\displaystyle \ln \left[1-(I_{1}-3)x\right]}$ around ${\displaystyle x=0}$ and taking the limit as ${\displaystyle x\rightarrow 0}$ leads to

${\displaystyle W={\cfrac {\mu }{2}}(I_{1}-3)}$

which is the expression for the strain energy density of a Neo-Hookean solid.

Several compressible versions of the Gent model have been designed. One such model has the form[2] (the below strain energy function yields a non zero hydrostatic stress at no deformation, refer https://link.springer.com/article/10.1007/s10659-005-4408-x for compressible Gent models).

${\displaystyle W=-{\cfrac {\mu J_{m}}{2}}\ln \left(1-{\cfrac {I_{1}-3}{J_{m}}}\right)+{\cfrac {\kappa }{2}}\left({\cfrac {J^{2}-1}{2}}-\ln J\right)^{4}}$

where ${\displaystyle J=\det({\boldsymbol {F}})}$, ${\displaystyle \kappa }$ is the bulk modulus, and ${\displaystyle {\boldsymbol {F}}}$ is the deformation gradient.

Consistency condition

We may alternatively express the Gent model in the form

${\displaystyle W=C_{0}\ln \left(1-{\cfrac {I_{1}-3}{J_{m}}}\right)}$

For the model to be consistent with linear elasticity, the following condition has to be satisfied:

${\displaystyle 2{\cfrac {\partial W}{\partial I_{1}}}(3)=\mu }$

where ${\displaystyle \mu }$ is the shear modulus of the material. Now, at ${\displaystyle I_{1}=3(\lambda _{i}=\lambda _{j}=1)}$,

${\displaystyle {\cfrac {\partial W}{\partial I_{1}}}=-{\cfrac {C_{0}}{J_{m}}}}$

Therefore, the consistency condition for the Gent model is

${\displaystyle -{\cfrac {2C_{0}}{J_{m}}}=\mu \,\qquad \implies \qquad C_{0}=-{\cfrac {\mu J_{m}}{2}}}$

The Gent model assumes that ${\displaystyle J_{m}\gg 1}$

Stress-deformation relations

The Cauchy stress for the incompressible Gent model is given by

${\displaystyle {\boldsymbol {\sigma }}=-p~{\boldsymbol {\mathit {I}}}+2~{\cfrac {\partial W}{\partial I_{1}}}~{\boldsymbol {B}}=-p~{\boldsymbol {\mathit {I}}}+{\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}~{\boldsymbol {B}}}$

Uniaxial extension

Stress-strain curves under uniaxial extension for Gent model compared with various hyperelastic material models.

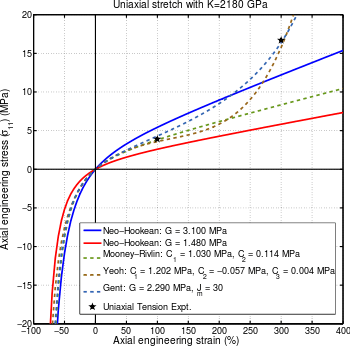
For uniaxial extension in the ${\displaystyle \mathbf {n} _{1}}$-direction, the principal stretches are ${\displaystyle \lambda _{1}=\lambda ,~\lambda _{2}=\lambda _{3}}$. From incompressibility ${\displaystyle \lambda _{1}~\lambda _{2}~\lambda _{3}=1}$. Hence ${\displaystyle \lambda _{2}^{2}=\lambda _{3}^{2}=1/\lambda }$. Therefore,

${\displaystyle I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=\lambda ^{2}+{\cfrac {2}{\sqrt {\lambda }}}~.}$

The left Cauchy-Green deformation tensor can then be expressed as

${\displaystyle {\boldsymbol {B}}=\lambda ^{2}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\cfrac {1}{\lambda }}~(\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\mathbf {n} _{3}\otimes \mathbf {n} _{3})~.}$

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

${\displaystyle \sigma _{11}=-p+{\cfrac {\lambda ^{2}\mu J_{m}}{J_{m}-I_{1}+3}}~;~~\sigma _{22}=-p+{\cfrac {\mu J_{m}}{\lambda (J_{m}-I_{1}+3)}}=\sigma _{33}~.}$

If ${\displaystyle \sigma _{22}=\sigma _{33}=0}$, we have

${\displaystyle p={\cfrac {\mu J_{m}}{\lambda (J_{m}-I_{1}+3)}}~.}$

Therefore,

${\displaystyle \sigma _{11}=\left(\lambda ^{2}-{\cfrac {1}{\lambda }}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~.}$

The engineering strain is ${\displaystyle \lambda -1\,}$. The engineering stress is

${\displaystyle T_{11}=\sigma _{11}/\lambda =\left(\lambda -{\cfrac {1}{\lambda ^{2}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~.}$

Equibiaxial extension

For equibiaxial extension in the ${\displaystyle \mathbf {n} _{1}}$ and ${\displaystyle \mathbf {n} _{2}}$ directions, the principal stretches are ${\displaystyle \lambda _{1}=\lambda _{2}=\lambda \,}$. From incompressibility ${\displaystyle \lambda _{1}~\lambda _{2}~\lambda _{3}=1}$. Hence ${\displaystyle \lambda _{3}=1/\lambda ^{2}\,}$. Therefore,

${\displaystyle I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=2~\lambda ^{2}+{\cfrac {1}{\lambda ^{4}}}~.}$

The left Cauchy-Green deformation tensor can then be expressed as

${\displaystyle {\boldsymbol {B}}=\lambda ^{2}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda ^{2}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+{\cfrac {1}{\lambda ^{4}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}~.}$

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

${\displaystyle \sigma _{11}=\left(\lambda ^{2}-{\cfrac {1}{\lambda ^{4}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)=\sigma _{22}~.}$

The engineering strain is ${\displaystyle \lambda -1\,}$. The engineering stress is

${\displaystyle T_{11}={\cfrac {\sigma _{11}}{\lambda }}=\left(\lambda -{\cfrac {1}{\lambda ^{5}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)=T_{22}~.}$

Planar extension

Planar extension tests are carried out on thin specimens which are constrained from deforming in one direction. For planar extension in the ${\displaystyle \mathbf {n} _{1}}$ directions with the ${\displaystyle \mathbf {n} _{3}}$ direction constrained, the principal stretches are ${\displaystyle \lambda _{1}=\lambda ,~\lambda _{3}=1}$. From incompressibility ${\displaystyle \lambda _{1}~\lambda _{2}~\lambda _{3}=1}$. Hence ${\displaystyle \lambda _{2}=1/\lambda \,}$. Therefore,

${\displaystyle I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=\lambda ^{2}+{\cfrac {1}{\lambda ^{2}}}+1~.}$

The left Cauchy-Green deformation tensor can then be expressed as

${\displaystyle {\boldsymbol {B}}=\lambda ^{2}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\cfrac {1}{\lambda ^{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\mathbf {n} _{3}\otimes \mathbf {n} _{3}~.}$

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

${\displaystyle \sigma _{11}=\left(\lambda ^{2}-{\cfrac {1}{\lambda ^{2}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~;~~\sigma _{22}=0~;~~\sigma _{33}=\left(1-{\cfrac {1}{\lambda ^{2}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~.}$

The engineering strain is ${\displaystyle \lambda -1\,}$. The engineering stress is

${\displaystyle T_{11}={\cfrac {\sigma _{11}}{\lambda }}=\left(\lambda -{\cfrac {1}{\lambda ^{3}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~.}$

Simple shear

The deformation gradient for a simple shear deformation has the form[3]

${\displaystyle {\boldsymbol {F}}={\boldsymbol {1}}+\gamma ~\mathbf {e} _{1}\otimes \mathbf {e} _{2}}$

where ${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2}}$ are reference orthonormal basis vectors in the plane of deformation and the shear deformation is given by

${\displaystyle \gamma =\lambda -{\cfrac {1}{\lambda }}~;~~\lambda _{1}=\lambda ~;~~\lambda _{2}={\cfrac {1}{\lambda }}~;~~\lambda _{3}=1}$

In matrix form, the deformation gradient and the left Cauchy-Green deformation tensor may then be expressed as

${\displaystyle {\boldsymbol {F}}={\begin{bmatrix}1&\gamma &0\\0&1&0\\0&0&1\end{bmatrix}}~;~~{\boldsymbol {B}}={\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}={\begin{bmatrix}1+\gamma ^{2}&\gamma &0\\\gamma &1&0\\0&0&1\end{bmatrix}}}$

Therefore,

${\displaystyle I_{1}=\mathrm {tr} ({\boldsymbol {B}})=3+\gamma ^{2}}$

and the Cauchy stress is given by

${\displaystyle {\boldsymbol {\sigma }}=-p~{\boldsymbol {\mathit {1}}}+{\cfrac {\mu J_{m}}{J_{m}-\gamma ^{2}}}~{\boldsymbol {B}}}$

In matrix form,

${\displaystyle {\boldsymbol {\sigma }}={\begin{bmatrix}-p+{\cfrac {\mu J_{m}(1+\gamma ^{2})}{J_{m}-\gamma ^{2}}}&{\cfrac {\mu J_{m}\gamma }{J_{m}-\gamma ^{2}}}&0\\{\cfrac {\mu J_{m}\gamma }{J_{m}-\gamma ^{2}}}&-p+{\cfrac {\mu J_{m}}{J_{m}-\gamma ^{2}}}&0\\0&0&-p+{\cfrac {\mu J_{m}}{J_{m}-\gamma ^{2}}}\end{bmatrix}}}$

References

1. Gent, A.N., 1996, A new constitutive relation for rubber, Rubber Chemistry Tech., 69, pp. 59-61.
2. Mac Donald, B. J., 2007, Practical stress analysis with finite elements, Glasnevin, Ireland.
3. Ogden, R. W., 1984, Non-linear elastic deformations, Dover.

See also

• Hyperelastic material
• Strain energy density function
• Mooney-Rivlin solid
• Finite strain theory
• Stress measures