Final topology

In general topology and related areas of mathematics, the final topology (or coinduced,[1] strong, colimit, or inductive topology) on a set ${\displaystyle X}$, with respect to a family of functions into ${\displaystyle X}$, is the finest topology on ${\displaystyle X}$ that makes those functions continuous.

The dual notion is the initial topology, which for a given family of functions from a set ${\displaystyle X}$ is the coarsest topology on ${\displaystyle X}$ that makes those functions continuous.

Definition

Given a set ${\displaystyle X}$ and a family of topological spaces ${\displaystyle Y_{i}}$ with functions

${\displaystyle f_{i}\colon Y_{i}\to X,}$

the final topology ${\displaystyle \tau }$ on ${\displaystyle X}$ is the finest topology such that each

${\displaystyle f_{i}\colon Y_{i}\to (X,\tau )}$

is continuous. Explicitly, the final topology may be described as follows: a subset U of X is open if and only if ${\displaystyle f_{i}^{-1}(U)}$ is open in ${\displaystyle Y_{i}}$ for each ${\displaystyle i\in I}$.

Examples

• The quotient topology is the final topology on the quotient space with respect to the quotient map.
• The disjoint union is the final topology with respect to the family of canonical injections.
• More generally, a topological space is coherent with a family of subspaces if it has the final topology coinduced by the inclusion maps.
• The direct limit of any direct system of spaces and continuous maps is the set-theoretic direct limit together with the final topology determined by the canonical morphisms.
• Given a family of topologies ${\displaystyle \{\tau _{i}\}}$ on a fixed set X, the final topology on X with respect to the functions ${\displaystyle \operatorname {id} _{X}\colon (X,\tau _{i})\to X}$ is the infimum (or meet) of the topologies ${\displaystyle \{\tau _{i}\}}$ in the lattice of topologies on X. That is, the final topology τ is the intersection of the topologies ${\displaystyle \{\tau _{i}\}}$.
• The étalé space of a sheaf is topologized by a final topology.

Properties

A subset of ${\displaystyle X}$ is closed/open if and only if its preimage under f_i is closed/open in ${\displaystyle Y_{i}}$ for each i ∈ I.

The final topology on X can be characterized by the following characteristic property: a function ${\displaystyle g}$ from ${\displaystyle X}$ to some space ${\displaystyle Z}$ is continuous if and only if ${\displaystyle g\circ f_{i}}$ is continuous for each i ∈ I.

Characteristic property of the final topology

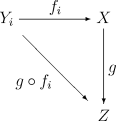
By the universal property of the disjoint union topology we know that given any family of continuous maps f_i : Y_i → X, there is a unique continuous map

${\displaystyle f\colon \coprod _{i}Y_{i}\to X.}$

If the family of maps f_i covers X (i.e. each x in X lies in the image of some f_i) then the map f will be a quotient map if and only if X has the final topology determined by the maps f_i.

Categorical description

In the language of category theory, the final topology construction can be described as follows. Let Y be a functor from a discrete category J to the category of topological spaces Top that selects the spaces Y_i for i in J. Let Δ be the diagonal functor from Top to the functor category Top^J (this functor sends each space X to the constant functor to X). The comma category (Y ↓ Δ) is then the category of cones from Y, i.e. objects in (Y ↓ Δ) are pairs (X, f) where f_i : Y_i → X is a family of continuous maps to X. If U is the forgetful functor from Top to Set and Δ′ is the diagonal functor from Set to Set^J then the comma category (UY ↓ Δ′) is the category of all cones from UY. The final topology construction can then be described as a functor from (UY ↓ Δ′) to (Y ↓ Δ). This functor is left adjoint to the corresponding forgetful functor.

See also

• Initial topology
• Induced topology

References

1. Singh, Tej Bahadur (May 5, 2013). "Elements of Topology". Books.Google.com. CRC Press. Retrieved July 21, 2020.

Sources

• Willard, Stephen (1970). General Topology. Addison-Wesley Series in Mathematics. Reading, MA: Addison-Wesley. Zbl 0205.26601.. (Provides a short, general introduction in section 9 and Exercise 9H)