Fibrifold

In mathematics, a fibrifold is (roughly) a fiber space whose fibers and base spaces are orbifolds. They were introduced by John Horton Conway, Olaf Delgado Friedrichs, and Daniel H. Huson et al. (2001), who introduced a system of notation for 3-dimensional fibrifolds and used this to assign names to the 219 affine space group types. 184 of these are considered reducible, and 35 irreducible.

Irreducible cubic space groups

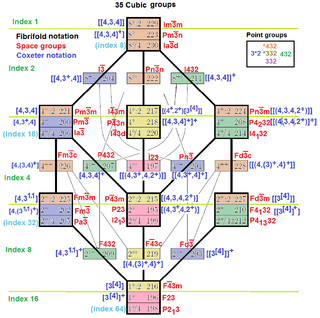
The 35/36 irreducible cubic space groups, in fibrifold and international index, and Hermann–Mauguin notation in red. 212 and 213 are enantiomorphous pairs giving the same fibrifold notation. Subgroup indices 1,2,4,8,16 are partitioned from top to bottom, with /4 groups (in blue) with their indices times 4.

The 35 irreducible space groups correspond to the cubic space group.

35 irreducible space groups
8^o:2	4⁻:2	4^o:2	4⁺:2	2⁻:2	2^o:2	2⁺:2	1^o:2
8^o	4⁻	4^o	4⁺	2⁻	2^o	2⁺	1^o
8^o/4	4⁻/4	4^o/4	4⁺/4	2⁻/4	2^o/4	2⁺/4	1^o/4
8^−o	8^oo	8^+o	4^{− −}	4^−o	4^oo	4^+o	4⁺⁺	2^−o	2^oo	2^+o

36 cubic groups
Class Point group	Hexoctahedral *432 (m3m)	Hextetrahedral *332 (43m)	Gyroidal 432 (432)	Diploidal 3*2 (m3)	Tetartoidal 332 (23)
bc lattice (I)	8^o:2 (Im3m)	4^o:2 (I43m)	8^+o (I432)	8^−o (I3)	4^oo (I23)
nc lattice (P)	4⁻:2 (Pm3m)	2^o:2 (P43m)	4^−o (P432)	4⁻ (Pm3)	2^o (P23)
nc lattice (P)	4⁺:2 (Pn3m)	2^o:2 (P43m)	4⁺ (P4₂32)	4^+o (Pn3)	2^o (P23)
fc lattice (F)	2⁻:2 (Fm3m)	1^o:2 (F43m)	2^−o (F432)	2⁻ (Fm3)	1^o (F23)
fc lattice (F)	2⁺:2 (Fd3m)	1^o:2 (F43m)	2⁺ (F4₁32)	2^+o (Fd3)	1^o (F23)
Other lattice groups	8^o (Pm3n) 8^oo (Pn3n) 4^{− −} (Fm3c) 4⁺⁺ (Fd3c)	4^o (P43n) 2^oo (F43c)
Achiral quarter groups	8^o/4 (Ia3d)	4^o/4 (I43d)	4⁺/4 (I4₁32) 2⁺/4 (P4₃32, P4₁32)	2⁻/4 (Pa3) 4⁻/4 (Ia3)	1^o/4 (P2₁3) 2^o/4 (I2₁3)


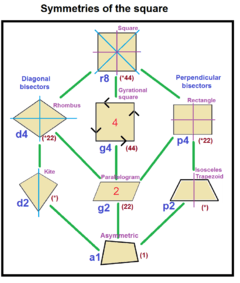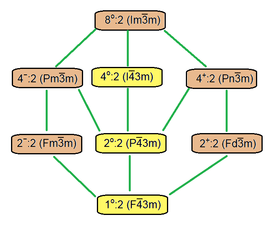
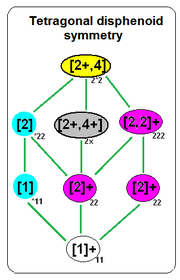
8 primary hexoctahedral hextetrahedral lattices of the cubic space groups	The fibrifold cubic subgroup structure shown is based on extending symmetry of the tetragonal disphenoid fundamental domain of space group 216, similar to the square

Irreducible group symbols (indexed 195−230) in Hermann–Mauguin notation, Fibrifold notation, geometric notation, and Coxeter notation:

Class (Orbifold point group)	Space groups
Tetartoidal 23 (332)	195	196	197	198	199
	P23	F23	I23	P2₁3	I2₁3
	2^o	1^o	4^oo	1^o/4	2^o/4
	P3.3.2	F3.3.2	I3.3.2	P3.3.2₁	I3.3.2₁
	[(4,3⁺,4,2⁺)]	[3^[4]]⁺	[[(4,3<sup>+</sup>,4,2<sup>+</sup>)]]
Diploidal 43m (3*2)	200	201	202	203	204	205	206
	Pm3	Pn3	Fm3	Fd3	I3	Pa3	Ia3
	4⁻	4^+o	2⁻	2^+o	8^−o	2⁻/4	4⁻/4
	P43	P_n43	F43	F_d43	I43	P_b43	I_b43
	[4,3⁺,4]	[[4,3⁺,4]⁺]	[4,(3^1,1)⁺]	[[3^[4]]]⁺	[[4,3⁺,4]]
Gyroidal 432 (432)	207	208	209	210	211	212	213	214
	P432	P4₂32	F432	F4₁32	I432	P4₃32	P4₁32	I4₁32
	4^−o	4⁺	2^−o	2⁺	8^+o	2⁺/4		4⁺/4
	P4.3.2	P4₂.3.2	F4.3.2	F4₁.3.2	I4.3.2	P4₃.3.2	P4₁.3.2	I4₁.3.2
	[4,3,4]⁺	[[4,3,4]⁺]⁺	[4,3^1,1]⁺	[[3^[4]]]⁺	[[4,3,4]]⁺
Hextetrahedral 43m (*332)	215	216	217	218	219	220
	P43m	F43m	I43m	P43n	F43c	I43d
	2^o:2	1^o:2	4^o:2	4^o	2^oo	4^o/4
	P33	F33	I33	P_n3_n3_n	F_c3_c3_a	I_d3_d3_d
	[(4,3,4,2⁺)]	[3^[4]]	[[(4,3,4,2⁺)]]	[[(4,3,4,2⁺)]⁺]	[⁺(4,{3),4}⁺]
Hexoctahedral m3m (*432)	221	222	223	224	225	226	227	228	229	230
	Pm3m	Pn3n	Pm3n	Pn3m	Fm3m	Fm3c	Fd3m	Fd3c	Im3m	Ia3d
	4⁻:2	8^oo	8^o	4⁺:2	2⁻:2	4⁻⁻	2⁺:2	4⁺⁺	8^o:2	8^o/4
	P43	P_n4_n3_n	P4_n3_n	P_n43	F43	F4_c3_a	F_d4_n3	F_d4_c3_a	I43	I_b4_d3_d
	[4,3,4]		[[4,3,4]⁺]	[(4⁺,2⁺)[3^[4]]]	[4,3^1,1]	[4,(3,4)⁺]	[[3^[4]]]	[[⁺(4,{3),4}⁺]]	[[4,3,4]]

gollark: Just buy a RX 570 or something.

gollark: Specifically the common Mekanism lasers.

gollark: If you want a space battle, definitely. It might cause problems with common späce weaponry though.

gollark: I hope we can do the space battle lateish so the Blorg cube can be made.

gollark: I think the best method would just be to stick maintenence tunnels under all the hallways and run all cables in them.

References

Conway, John Horton; Delgado Friedrichs, Olaf; Huson, Daniel H.; Thurston, William P. (2001), "On three-dimensional space groups", Beiträge zur Algebra und Geometrie. Contributions to Algebra and Geometry, 42 (2): 475–507, ISSN 0138-4821, MR 1865535
Hestenes, David; Holt, Jeremy W. (February 2007), "The Crystallographic Space Groups in Geometric Algebra" (PDF), Journal of Mathematical Physics, 48 (2): 023514, doi:10.1063/1.2426416
Huson, Daniel H. (2008), The Fibrifold Notation and Classification for 3D Space Groups (PDF)
Conway, John H.; Burgiel, Heidi; Goodman-Strass, Chaim (2008), The Symmetries of Things, Taylor & Francis, ISBN 978-1-56881-220-5, Zbl 1173.00001
Coxeter, H.S.M. (1995), "Regular and Semi Regular Polytopes III", in Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; et al. (eds.), Kaleidoscopes: Selected Writings of H.S.M. Coxeter, Wiley, pp. 313–358, ISBN 978-0-471-01003-6, Zbl 0976.01023

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.