Feynman checkerboard

The Feynman checkerboard, or relativistic chessboard model, was Richard Feynman’s sum-over-paths formulation of the kernel for a free spin-½ particle moving in one spatial dimension. It provides a representation of solutions of the Dirac equation in (1+1)-dimensional spacetime as discrete sums.

Feynman checkerboard with two paths contributing to the sum for the propagator from (${\displaystyle x/\epsilon c}$, ${\displaystyle t/\epsilon }$) = (0, 0) to (3, 7)

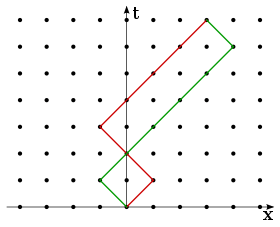
The model can be visualised by considering relativistic random walks on a two-dimensional spacetime checkerboard. At each discrete timestep ${\displaystyle \epsilon }$ the particle of mass ${\displaystyle m}$ moves a distance ${\displaystyle \epsilon c}$ to the left or right (${\displaystyle c}$ being the speed of light). For such a discrete motion, the Feynman path integral reduces to a sum over the possible paths. Feynman demonstrated that if each "turn" (change of moving from left to right or conversely) of the space–time path is weighted by ${\displaystyle -i\epsilon mc^{2}/\hbar }$ (with ${\displaystyle \hbar }$ denoting the reduced Planck's constant), in the limit of infinitely small checkerboard squares the sum of all weighted paths yields a propagator that satisfies the one-dimensional Dirac equation. As a result, helicity (the one-dimensional equivalent of spin) is obtained from a simple cellular-automata-type rule.

The checkerboard model is important because it connects aspects of spin and chirality with propagation in spacetime[1] and is the only sum-over-path formulation in which quantum phase is discrete at the level of the paths, taking only values corresponding to the 4th roots of unity.

History

Feynman invented the model in the 1940s while developing his spacetime approach to quantum mechanics.[2] He did not publish the result until it appeared in a text on path integrals coauthored by Albert Hibbs in the mid 1960s.[3] The model was not included with the original path-integral article[2] because a suitable generalization to a four-dimensional spacetime had not been found.[4]

One of the first connections between the amplitudes prescribed by Feynman for the Dirac particle in 1+1 dimensions, and the standard interpretation of amplitudes in terms of the kernel, or propagator, was established by Jayant Narlikar in a detailed analysis.[5] The name "Feynman chessboard model" was coined by Gersch when he demonstrated its relationship to the one-dimensional Ising model.[6] Gaveau et al. discovered a relationship between the model and a stochastic model of the telegraph equations due to Mark Kac through analytic continuation.[7] Jacobson and Schulman examined the passage from the relativistic to the non-relativistic path integral.[8] Subsequently, Ord showed that the Chessboard model was embedded in correlations in Kac's original stochastic model[9] and so had a purely classical context, free of formal analytic continuation.[10] In the same year, Kauffman and Noyes[11] produced a fully discrete version related to bit-string physics, which has been developed into a general approach to discrete physics.[12]

Extensions

Although Feynman did not live to publish extensions to the chessboard model, it is evident from his archived notes that he was interested in establishing a link between the 4th roots of unity (used as statistical weights in chessboard paths) and his discovery, with J. A. Wheeler, that antiparticles are equivalent to particles moving backwards in time.[1] His notes contain several sketches of chessboard paths with added spacetime loops.[13] The first extension of the model to explicitly contain such loops was the "spiral model", in which chessboard paths were allowed to spiral in spacetime. Unlike the chessboard case, causality had to be implemented explicitly to avoid divergences, however with this restriction the Dirac equation emerged as a continuum limit.[14] Subsequently, the roles of zitterbewegung, antiparticles and the Dirac sea in the chessboard model have been elucidated,[15] and the implications for the Schrödinger equation considered through the non-relativistic limit.[16]

Further extensions of the original 2-dimensional spacetime model include features such as improved summation rules[17] and generalized lattices.[18] There has been no consensus on an optimal extension of the chessboard model to a fully four-dimensional space-time. Two distinct classes of extensions exist, those working with a fixed underlying lattice[19][20] and those that embed the two-dimensional case in higher dimension.[21][22] The advantage of the former is that the sum-over-paths is closer to the non-relativistic case, however the simple picture of a single directionally independent speed of light is lost. In the latter extensions the fixed-speed property is maintained at the expense of variable directions at each step.

References

1. Schweber, Silvan S. (1994). QED and the men who made it. Princeton University Press.
2. Feynman, R. P. (1948-04-01). "Space-Time Approach to Non-Relativistic Quantum Mechanics". Reviews of Modern Physics. American Physical Society (APS). 20 (2): 367–387. doi:10.1103/revmodphys.20.367. ISSN 0034-6861.
3. Feynman and Hibbs, Quantum Mechanics and Path Integrals, New York: McGraw-Hill, Problem 2-6, pp. 34–36, 1965.
4. R. P. Feynman, The Development of the Space-Time View of Quantum Electrodynamics, Science, 153, pp. 699–708, 1966 (Reprint of the Nobel Prize lecture).
5. J. Narlikar, Path Amplitudes for Dirac particles, Journal of the Indian Mathematical Society, 36, pp. 9–32, 1972.
6. Gersch, H. A. (1981). "Feynman's relativistic chessboard as an ising model". International Journal of Theoretical Physics. Springer Nature. 20 (7): 491–501. doi:10.1007/bf00669436. ISSN 0020-7748.
7. Gaveau, B.; Jacobson, T.; Kac, M.; Schulman, L. S. (1984-07-30). "Relativistic Extension of the Analogy between Quantum Mechanics and Brownian Motion". Physical Review Letters. American Physical Society (APS). 53 (5): 419–422. doi:10.1103/physrevlett.53.419. ISSN 0031-9007.
8. Jacobson, T; Schulman, L S (1984-02-01). "Quantum stochastics: the passage from a relativistic to a non-relativistic path integral". Journal of Physics A: Mathematical and General. IOP Publishing. 17 (2): 375–383. doi:10.1088/0305-4470/17/2/023. ISSN 0305-4470.
9. Kac, Mark (1974). "A stochastic model related to the telegrapher's equation". Rocky Mountain Journal of Mathematics. Rocky Mountain Mathematics Consortium. 4 (3): 497–510. doi:10.1216/rmj-1974-4-3-497. ISSN 0035-7596.
10. Ord, G.N. (1996). "The Schrödinger and Dirac Free Particle Equations without Quantum Mechanics". Annals of Physics. Elsevier BV. 250 (1): 51–62. doi:10.1006/aphy.1996.0087. ISSN 0003-4916.
11. Kauffman, Louis H.; Pierre Noyes, H. (1996). "Discrete physics and the Dirac equation". Physics Letters A. Elsevier BV. 218 (3–6): 139–146. arXiv:hep-th/9603202. doi:10.1016/0375-9601(96)00436-7. ISSN 0375-9601.
12. Louis H. Kauffman, Non-Commutative Worlds – A Summary, 2005, arXiv:quant-ph/0503198.
13. Schweber, Silvan S. (1986-04-01). "Feynman and the visualization of space-time processes". Reviews of Modern Physics. American Physical Society (APS). 58 (2): 449–508. doi:10.1103/revmodphys.58.449. ISSN 0034-6861.
14. Ord, G. N. (1992). "Classical analog of quantum phase". International Journal of Theoretical Physics. Springer Nature. 31 (7): 1177–1195. doi:10.1007/bf00673919. ISSN 0020-7748.
15. Ord, G. N.; Gualtieri, J. A. (2002-12-02). "The Feynman Propagator from a Single Path". Physical Review Letters. 89 (25): 250403–250407. arXiv:quant-ph/0109092. doi:10.1103/physrevlett.89.250403. ISSN 0031-9007. PMID 12484870.
16. Ord, G.N.; Mann, R.B. (2003). "Entwined pairs and Schrödinger's equation". Annals of Physics. Elsevier BV. 308 (2): 478–492. arXiv:quant-ph/0206095. doi:10.1016/s0003-4916(03)00148-9. ISSN 0003-4916.
17. Kull, Andreas; Treumann, R. A. (1999). "On the path integral of the relativistic electron". International Journal of Theoretical Physics. 38 (5): 1423–1428. arXiv:quant-ph/9901058. doi:10.1023/a:1026637015146. ISSN 0020-7748.
18. Kull, Andreas (2002). "Quantum mechanical motion of relativistic particle in non-continuous spacetime". Physics Letters A. 303 (2–3): 147–153. arXiv:quant-ph/0212053. doi:10.1016/s0375-9601(02)01238-0. ISSN 0375-9601.
19. Jacobson, T. (1985). "Feynman's checkerboard and other games". Non-Linear Equations in Classical and Quantum Field Theory. Lecture Notes in Physics. 226. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 386–395. doi:10.1007/3-540-15213-x_88. ISBN 978-3-540-15213-2.
20. Frank D. Smith, HyperDiamond Feynman Checkerboard in 4-dimensional Spacetime, 1995, arXiv:quant-ph/9503015
21. Ord, G.N.; Mckeon, D.G.C. (1993). "On the Dirac Equation in 3 + 1 Dimensions". Annals of Physics. Elsevier BV. 222 (2): 244–253. doi:10.1006/aphy.1993.1022. ISSN 0003-4916.
22. Rosen, Gerald (1983-08-01). "Feynman path summation for the Dirac equation: An underlying one-dimensional aspect of relativistic particle motion". Physical Review A. American Physical Society (APS). 28 (2): 1139–1140. doi:10.1103/physreva.28.1139. ISSN 0556-2791.