Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues.[1] A queueing model is constructed so that queue lengths and waiting time can be predicted.[1] Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service.
Queueing theory has its origins in research by Agner Krarup Erlang when he created models to describe the Copenhagen telephone exchange.[1] The ideas have since seen applications including telecommunication, traffic engineering, computing[2] and, particularly in industrial engineering, in the design of factories, shops, offices and hospitals, as well as in project management.[3][4]
Birth-death process
The behaviour / state of a single queue (also called a "queueing node") can be described by a birth-death process, which describes the arrivals and departures from the queue, along with the number of jobs (also called "customers" or "requests", or any number of other things, depending on the field) currently in the system. An arrival increases the number of jobs by 1, and a departure (a job completing its service) decreases k by 1 (see Fig. 3).
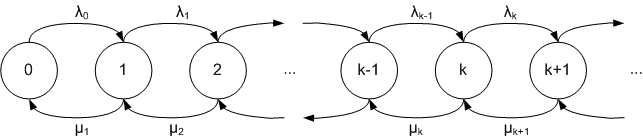

The steady state equations for birth-and-death process are as follows. (Here denotes the steady state probability to be in state n.)
- Balance equations
- equation for state 1 (via state 0):
- equation for state 2 (via states 0 and 1):
- general equation (expressing state n + 1 via states n − 1,n):
- From the first two equations we have:
- By mathematical induction we arrive at the formula
- From the condition
- we obtain
- which together with the equation for fully describes the required steady state probabilities.
Example analysis of an M/M/1 queue
Consider a queue with 1 server and the following variables:
- λ: the arrival rate (the expected time between each customer arriving, e.g. 30 seconds);
- μ: the reciprocal of the mean service time (the expected number of consecutive service completions per the same unit time, e.g. per 30 seconds);
- n: the parameter characterizing the number of customers in the system;
- Pn: the probability of being n customers in the system in steady state.
Further, let En represent the number of times the system enters state n, and Ln represent the number of times the system leaves state n. For all n, we have |En − Ln| ∈ {0, 1}, that is, the number of times the system leaves a state differs by at most 1 from the number of times it enters that state, since it will either return into that state at some time in the future (En = Ln) or not (|En − Ln| = 1).
When the system arrives at a steady state, the arrival rate should be equal to the departure rate.
- Balance equations
- equation for state 1 (via state 0):
- equation for state 2 (via states 0 and 1):
- general equation (describing state n + 1 via states n and n − 1):
- We have:
- Taking into account that , we finally arrive at the geometric distribution formula where
Simple two-equation queue
A common basic queuing system is attributed to Erlang, and is a modification of Little's Law. Given an arrival rate λ, a dropout rate σ, and a departure rate μ, length of the queue L is defined as:
Assuming an exponential distribution for the rates, the waiting time W can be defined as the proportion of arrivals that are served. This is equal to the exponential survival rate of those who do not drop out over the waiting period, giving:
The second equation is commonly rewritten as:
The two-stage one-box model is common in epidemiology.[5]
Kendall's notation
Single queueing nodes are usually described using Kendall's notation in the form A/S/c where A describes the distribution of durations between each arrival to the queue, S the distribution of service times for jobs and c the number of servers at the node.[6][7] For an example of the notation, the M/M/1 queue is a simple model where a single server serves jobs that arrive according to a Poisson process (inter-arrival durations are exponentially distributed) and have exponentially distributed service times. In an M/G/1 queue, the G stands for general and indicates an arbitrary probability distribution for service times.
Overview of the development of the theory
In 1909, Agner Krarup Erlang, a Danish engineer who worked for the Copenhagen Telephone Exchange, published the first paper on what would now be called queueing theory.[8][9][10] He modeled the number of telephone calls arriving at an exchange by a Poisson process and solved the M/D/1 queue in 1917 and M/D/k queueing model in 1920.[11] In Kendall's notation:
- M stands for Markov or memoryless and means arrivals occur according to a Poisson process;
- D stands for deterministic and means jobs arriving at the queue which require a fixed amount of service;
- k describes the number of servers at the queueing node (k = 1, 2, ...).
If there are more jobs at the node than there are servers, then jobs will queue and wait for service
The M/G/1 queue was solved by Felix Pollaczek in 1930,[12] a solution later recast in probabilistic terms by Aleksandr Khinchin and now known as the Pollaczek–Khinchine formula.[11][13]
After the 1940s queueing theory became an area of research interest to mathematicians.[13] In 1953 David George Kendall solved the GI/M/k queue[14] and introduced the modern notation for queues, now known as Kendall's notation. In 1957 Pollaczek studied the GI/G/1 using an integral equation.[15] John Kingman gave a formula for the mean waiting time in a G/G/1 queue: Kingman's formula.[16]
Leonard Kleinrock worked on the application of queueing theory to message switching (in the early 1960s) and packet switching (in the early 1970s). His initial contribution to this field was his doctoral thesis at the Massachusetts Institute of Technology in 1962, published in book form in 1964 in the field of message switching. His theoretical work published in the early 1970s underpinned the use of packet switching in the ARPANET, a forerunner to the Internet.
The matrix geometric method and matrix analytic methods have allowed queues with phase-type distributed inter-arrival and service time distributions to be considered.[17]
Problems such as performance metrics for the M/G/k queue remain an open problem.[11][13]
Service disciplines
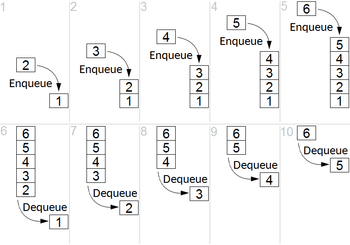
Various scheduling policies can be used at queuing nodes:
- First in first out
- Also called first-come, first-served (FCFS),[18] this principle states that customers are served one at a time and that the customer that has been waiting the longest is served first.[19]
- Last in first out
- This principle also serves customers one at a time, but the customer with the shortest waiting time will be served first.[19] Also known as a stack.
- Processor sharing
- Service capacity is shared equally between customers.[19]
- Priority
- Customers with high priority are served first.[19] Priority queues can be of two types, non-preemptive (where a job in service cannot be interrupted) and preemptive (where a job in service can be interrupted by a higher-priority job). No work is lost in either model.[20]
- Shortest job first
- The next job to be served is the one with the smallest size
- Preemptive shortest job first
- The next job to be served is the one with the original smallest size[21]
- Shortest remaining processing time
- The next job to serve is the one with the smallest remaining processing requirement.[22]
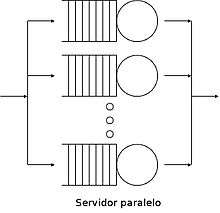
- Service facility
- Single server: customers line up and there is only one server
- Several parallel servers–Single queue: customers line up and there are several servers
- Several servers–Several queues: there are many counters and customers can decide going where to queue
- Customer's behavior of waiting
- Balking: customers deciding not to join the queue if it is too long
- Jockeying: customers switch between queues if they think they will get served faster by doing so
- Reneging: customers leave the queue if they have waited too long for service
Arriving customers not served (either due to the queue having no buffer, or due to balking or reneging by the customer) are also known as dropouts and the average rate of dropouts is a significant parameter describing a queue.
Heavy traffic/diffusion approximations
In a system with high occupancy rates (utilisation near 1) a heavy traffic approximation can be used to approximate the queueing length process by a reflected Brownian motion,[23] Ornstein–Uhlenbeck process or more general diffusion process.[24] The number of dimensions of the RBM is equal to the number of queueing nodes and the diffusion is restricted to the non-negative orthant.
Queueing networks
Networks of queues are systems in which a number of queues are connected by what's known as customer routing. When a customer is serviced at one node it can join another node and queue for service, or leave the network.
For networks of m nodes, the state of the system can be described by an m–dimensional vector (x1, x2, ..., xm) where xi represents the number of customers at each node.
The simplest non-trivial network of queues is called tandem queues.[25] The first significant results in this area were Jackson networks,[26][27] for which an efficient product-form stationary distribution exists and the mean value analysis[28] which allows average metrics such as throughput and sojourn times to be computed.[29] If the total number of customers in the network remains constant the network is called a closed network and has also been shown to have a product–form stationary distribution in the Gordon–Newell theorem.[30] This result was extended to the BCMP network[31] where a network with very general service time, regimes and customer routing is shown to also exhibit a product-form stationary distribution. The normalizing constant can be calculated with the Buzen's algorithm, proposed in 1973.[32]
Networks of customers have also been investigated, Kelly networks where customers of different classes experience different priority levels at different service nodes.[33] Another type of network are G-networks first proposed by Erol Gelenbe in 1993:[34] these networks do not assume exponential time distributions like the classic Jackson Network.
Routing algorithms
In discrete time networks where there is a constraint on which service nodes can be active at any time, the max-weight scheduling algorithm chooses a service policy to give optimal throughput in the case that each job visits only a single person [18] service node. In the more general case where jobs can visit more than one node, backpressure routing gives optimal throughput. A network scheduler must choose a queuing algorithm, which affects the characteristics of the larger network. See also Stochastic scheduling for more about scheduling of queueing systems.
Mean field limits
Mean field models consider the limiting behaviour of the empirical measure (proportion of queues in different states) as the number of queues (m above) goes to infinity. The impact of other queues on any given queue in the network is approximated by a differential equation. The deterministic model converges to the same stationary distribution as the original model.[35]
Fluid limits
Fluid models are continuous deterministic analogs of queueing networks obtained by taking the limit when the process is scaled in time and space, allowing heterogeneous objects. This scaled trajectory converges to a deterministic equation which allows the stability of the system to be proven. It is known that a queueing network can be stable, but have an unstable fluid limit.[36]
See also
- Ehrenfest model
- Erlang unit
- G/G/1 queue
- Industrial engineering
- M/M/1 queue
- Network simulation
- Poisson distribution
- Project production management
- Queue area
- Queueing delay
- Queue management system
- Queuing Rule of Thumb
- Queueing Systems – a journal of queueing theory
- Random early detection
- Renewal theory
- Throughput
- Scheduling (computing)
- Traffic jam
- Traffic generation model
- Flow network
- Stochastic scheduling
References
- Sundarapandian, V. (2009). "7. Queueing Theory". Probability, Statistics and Queueing Theory. PHI Learning. ISBN 978-8120338449.
- Lawrence W. Dowdy, Virgilio A.F. Almeida, Daniel A. Menasce. "Performance by Design: Computer Capacity Planning by Example".
- Schlechter, Kira (March 2, 2009). "Hershey Medical Center to open redesigned emergency room". The Patriot-News.
- Mayhew, Les; Smith, David (December 2006). Using queuing theory to analyse completion times in accident and emergency departments in the light of the Government 4-hour target. Cass Business School. ISBN 978-1-905752-06-5. Retrieved 2008-05-20.
- Hernández-Suarez, Carlos (2010). "An application of queuing theory to SIS and SEIS epidemic models". Math. Biosci. 7 (4): 809–823. doi:10.3934/mbe.2010.7.809. PMID 21077709.
- Tijms, H.C, Algorithmic Analysis of Queues", Chapter 9 in A First Course in Stochastic Models, Wiley, Chichester, 2003
- Kendall, D. G. (1953). "Stochastic Processes Occurring in the Theory of Queues and their Analysis by the Method of the Imbedded Markov Chain". The Annals of Mathematical Statistics. 24 (3): 338–354. doi:10.1214/aoms/1177728975. JSTOR 2236285.
- "Agner Krarup Erlang (1878-1929) | plus.maths.org". Pass.maths.org.uk. 1997-04-30. Retrieved 2013-04-22.
- Asmussen, S. R.; Boxma, O. J. (2009). "Editorial introduction". Queueing Systems. 63 (1–4): 1–2. doi:10.1007/s11134-009-9151-8.
- Erlang, Agner Krarup (1909). "The theory of probabilities and telephone conversations" (PDF). NYT Tidsskrift for Matematik B. 20: 33–39. Archived from the original (PDF) on 2011-10-01.
- Kingman, J. F. C. (2009). "The first Erlang century—and the next". Queueing Systems. 63 (1–4): 3–4. doi:10.1007/s11134-009-9147-4.
- Pollaczek, F., Ueber eine Aufgabe der Wahrscheinlichkeitstheorie, Math. Z. 1930
- Whittle, P. (2002). "Applied Probability in Great Britain". Operations Research. 50 (1): 227–239. doi:10.1287/opre.50.1.227.17792. JSTOR 3088474.
- Kendall, D.G.:Stochastic processes occurring in the theory of queues and their analysis by the method of the imbedded Markov chain, Ann. Math. Stat. 1953
- Pollaczek, F., Problèmes Stochastiques posés par le phénomène de formation d'une queue
- Kingman, J. F. C.; Atiyah (October 1961). "The single server queue in heavy traffic". Mathematical Proceedings of the Cambridge Philosophical Society. 57 (4): 902. doi:10.1017/S0305004100036094. JSTOR 2984229.
- Ramaswami, V. (1988). "A stable recursion for the steady state vector in markov chains of m/g/1 type". Communications in Statistics. Stochastic Models. 4: 183–188. doi:10.1080/15326348808807077.
- Manuel, Laguna (2011). Business Process Modeling, Simulation and Design. Pearson Education India. p. 178. ISBN 9788131761359. Retrieved 6 October 2017.
- Penttinen A., Chapter 8 – Queueing Systems, Lecture Notes: S-38.145 - Introduction to Teletraffic Theory.
- Harchol-Balter, M. (2012). "Scheduling: Non-Preemptive, Size-Based Policies". Performance Modeling and Design of Computer Systems. pp. 499–507. doi:10.1017/CBO9781139226424.039. ISBN 9781139226424.
- Harchol-Balter, M. (2012). "Scheduling: Preemptive, Size-Based Policies". Performance Modeling and Design of Computer Systems. pp. 508–517. doi:10.1017/CBO9781139226424.040. ISBN 9781139226424.
- Harchol-Balter, M. (2012). "Scheduling: SRPT and Fairness". Performance Modeling and Design of Computer Systems. pp. 518–530. doi:10.1017/CBO9781139226424.041. ISBN 9781139226424.
- Chen, H.; Whitt, W. (1993). "Diffusion approximations for open queueing networks with service interruptions". Queueing Systems. 13 (4): 335. doi:10.1007/BF01149260.
- Yamada, K. (1995). "Diffusion Approximation for Open State-Dependent Queueing Networks in the Heavy Traffic Situation". The Annals of Applied Probability. 5 (4): 958–982. doi:10.1214/aoap/1177004602. JSTOR 2245101.
- http://www.stats.ox.ac.uk/~winkel/bs3a07l13-14.pdf#page=4
- Jackson, J. R. (1957). "Networks of Waiting Lines". Operations Research. 5 (4): 518–521. doi:10.1287/opre.5.4.518. JSTOR 167249.
- Jackson, James R. (Oct 1963). "Jobshop-like Queueing Systems". Management Science. 10 (1): 131–142. doi:10.1287/mnsc.1040.0268. JSTOR 2627213.
- Reiser, M.; Lavenberg, S. S. (1980). "Mean-Value Analysis of Closed Multichain Queuing Networks". Journal of the ACM. 27 (2): 313. doi:10.1145/322186.322195.
- Van Dijk, N. M. (1993). "On the arrival theorem for communication networks". Computer Networks and ISDN Systems. 25 (10): 1135–2013. doi:10.1016/0169-7552(93)90073-D.
- Gordon, W. J.; Newell, G. F. (1967). "Closed Queuing Systems with Exponential Servers". Operations Research. 15 (2): 254. doi:10.1287/opre.15.2.254. JSTOR 168557.
- Baskett, F.; Chandy, K. Mani; Muntz, R.R.; Palacios, F.G. (1975). "Open, closed and mixed networks of queues with different classes of customers". Journal of the ACM. 22 (2): 248–260. doi:10.1145/321879.321887.
- Buzen, J. P. (1973). "Computational algorithms for closed queueing networks with exponential servers" (PDF). Communications of the ACM. 16 (9): 527–531. doi:10.1145/362342.362345.
- Kelly, F. P. (1975). "Networks of Queues with Customers of Different Types". Journal of Applied Probability. 12 (3): 542–554. doi:10.2307/3212869. JSTOR 3212869.
- Gelenbe, Erol (Sep 1993). "G-Networks with Triggered Customer Movement". Journal of Applied Probability. 30 (3): 742–748. doi:10.2307/3214781. JSTOR 3214781.
- Bobbio, A.; Gribaudo, M.; Telek, M. S. (2008). "Analysis of Large Scale Interacting Systems by Mean Field Method". 2008 Fifth International Conference on Quantitative Evaluation of Systems. p. 215. doi:10.1109/QEST.2008.47. ISBN 978-0-7695-3360-5.
- Bramson, M. (1999). "A stable queueing network with unstable fluid model". The Annals of Applied Probability. 9 (3): 818–853. doi:10.1214/aoap/1029962815. JSTOR 2667284.
Further reading
- Gross, Donald; Carl M. Harris (1998). Fundamentals of Queueing Theory. Wiley. ISBN 978-0-471-32812-4. Online
- Zukerman, Moshe. Introduction to Queueing Theory and Stochastic Teletraffic Models (PDF).
- Deitel, Harvey M. (1984) [1982]. An introduction to operating systems (revisited first ed.). Addison-Wesley. p. 673. ISBN 978-0-201-14502-1. chap.15, pp. 380–412
- Newell, Gordron F. (1 June 1971). Applications of Queueing Theory. Chapman and Hall.
- Leonard Kleinrock, Information Flow in Large Communication Nets, (MIT, Cambridge, May 31, 1961) Proposal for a Ph.D. Thesis
- Leonard Kleinrock. Information Flow in Large Communication Nets(RLE Quarterly Progress Report, July 1961)
- Leonard Kleinrock. Communication Nets: Stochastic Message Flow and Delay(McGraw-Hill, New York, 1964)
- Kleinrock, Leonard (2 January 1975). Queueing Systems: Volume I – Theory. New York: Wiley Interscience. pp. 417. ISBN 978-0471491101.
- Kleinrock, Leonard (22 April 1976). Queueing Systems: Volume II – Computer Applications. New York: Wiley Interscience. pp. 576. ISBN 978-0471491118.
- Lazowska, Edward D.; John Zahorjan; G. Scott Graham; Kenneth C. Sevcik (1984). Quantitative System Performance: Computer System Analysis Using Queueing Network Models. Prentice-Hall, Inc. ISBN 978-0-13-746975-8.
External links
- Queueing theory calculator
- Teknomo's Queueing theory tutorial and calculators
- Office Fire Emergency Evacuation Simulation on YouTube
- Virtamo's Queueing Theory Course
- Myron Hlynka's Queueing Theory Page
- Queueing Theory Basics
- A free online tool to solve some classical queueing systems
- JMT: an open source graphical environment for queueing theory
- LINE: a general-purpose engine to solve queueing models
- What You Hate Most About Waiting in Line: (It’s not the length of the wait.), by Seth Stevenson, Slate, 2012 – popular introduction