F1 score

In statistical analysis of binary classification, the F₁ score (also F-score or F-measure) is a measure of a test's accuracy. It is calculated from the precision p and the recall r of the test, where the precision p is the number of correctly identified positive results divided by the number of all positive results, including those not identified correctly, and the recall, r, is the number of correctly identified positive results divided by the number of all samples that should have been identified as positive, the relevance.

"F score" redirects here. For the significance test, see F-test.

Precision and recall

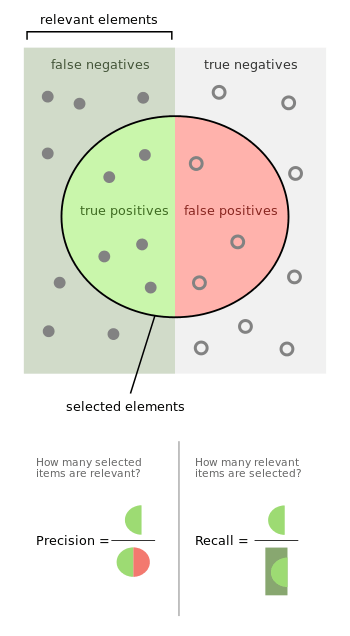
The F₁ score is the harmonic mean of the precision and recall. The highest possible value of F₁ is 1, indicating perfect precision and recall. The F₁ score is also known as the Sørensen–Dice coefficient or Dice similarity coefficient (DSC).

Etymology

The name F-measure is believed to be named after a different F function in Van Rijsbergen's book, when introduced to MUC-4. [1]

Definition

The traditional F-measure or balanced F-score (F₁ score) is the harmonic mean of precision and recall:

${\displaystyle F_{1}={\frac {2}{\mathrm {recall} ^{-1}+\mathrm {precision} ^{-1}}}=2\cdot {\frac {\mathrm {precision} \cdot \mathrm {recall} }{\mathrm {precision} +\mathrm {recall} }}={\frac {\mathrm {t} p}{\mathrm {tp} +{\frac {1}{2}}(\mathrm {fp} +\mathrm {fn} )}}}$.

${\displaystyle F_{\beta }}$

The general formula for positive real β, where β is chosen such that recall is considered β times as important as precision, is:

${\displaystyle F_{\beta }=(1+\beta ^{2})\cdot {\frac {\mathrm {precision} \cdot \mathrm {recall} }{(\beta ^{2}\cdot \mathrm {precision} )+\mathrm {recall} }}}$.

The formula in terms of Type I and type II errors:

${\displaystyle F_{\beta }={\frac {(1+\beta ^{2})\cdot \mathrm {true\ positive} }{(1+\beta ^{2})\cdot \mathrm {true\ positive} +\beta ^{2}\cdot \mathrm {false\ negative} +\mathrm {false\ positive} }}\,}$.

Two commonly used values for β are 2, which weighs recall higher than precision, and 0.5, which weighs recall lower than precision.

The F-measure was derived so that ${\displaystyle F_{\beta }}$ "measures the effectiveness of retrieval with respect to a user who attaches β times as much importance to recall as precision".[2] It is based on Van Rijsbergen's effectiveness measure

${\displaystyle E=1-\left({\frac {\alpha }{p}}+{\frac {1-\alpha }{r}}\right)^{-1}}$.

Their relationship is ${\displaystyle F_{\beta }=1-E}$ where ${\displaystyle \alpha ={\frac {1}{1+\beta ^{2}}}}$.

Diagnostic testing

This is related to the field of binary classification where recall is often termed "sensitivity".

		True condition
	Total population	Condition positive	Condition negative	Prevalence = Σ Condition positive/Σ Total population	Accuracy (ACC) = Σ True positive + Σ True negative/Σ Total population
Predicted condition	Predicted condition positive	True positive	False positive, Type I error	Positive predictive value (PPV), Precision = Σ True positive/Σ Predicted condition positive	False discovery rate (FDR) = Σ False positive/Σ Predicted condition positive
	Predicted condition negative	False negative, Type II error	True negative	False omission rate (FOR) = Σ False negative/Σ Predicted condition negative	Negative predictive value (NPV) = Σ True negative/Σ Predicted condition negative
		True positive rate (TPR), Recall, Sensitivity, probability of detection, Power = Σ True positive/Σ Condition positive	False positive rate (FPR), Fall-out, probability of false alarm = Σ False positive/Σ Condition negative	Positive likelihood ratio (LR+) = TPR/FPR	Diagnostic odds ratio (DOR) = LR+/LR−	F1 score = 2 · Precision · Recall/Precision + Recall
		False negative rate (FNR), Miss rate = Σ False negative/Σ Condition positive	Specificity (SPC), Selectivity, True negative rate (TNR) = Σ True negative/Σ Condition negative	Negative likelihood ratio (LR−) = FNR/TNR

Applications

The F-score is often used in the field of information retrieval for measuring search, document classification, and query classification performance.[3] Earlier works focused primarily on the F₁ score, but with the proliferation of large scale search engines, performance goals changed to place more emphasis on either precision or recall[4] and so ${\displaystyle F_{\beta }}$ is seen in wide application.

The F-score is also used in machine learning.[5] However, the F-measures do not take true negatives into account, hence measures such as the Matthews correlation coefficient, Informedness or Cohen's kappa may be prefered to assess the performance of a binary classifier.

The F-score has been widely used in the natural language processing literature,[6] such as in the evaluation of named entity recognition and word segmentation.

Criticism

David Hand and others criticize the widespread use of the F₁ score since it gives equal importance to precision and recall. In practice, different types of mis-classifications incur different costs. In other words, the relative importance of precision and recall is an aspect of the problem.[7]

According to Davide Chicco and Giuseppe Jurman, the F₁ score is less truthful and informative than the Matthews correlation coefficient (MCC) in binary evaluation classification.[8]

David Powers has pointed out that F1 ignores the True Negatives and thus is misleading for unbalanced classes, while kappa and correlation measures are symmetric and assess both directions of predictability - the classifier predicting the true class and the true class predicting the classifier prediction, proposing separate multiclass measures Informedness and Markedness for the two directions, noting that their geometric mean is correlation.[9]

Difference from Fowlkes–Mallows index

While the F-measure is the harmonic mean of recall and precision, the Fowlkes–Mallows index is their geometric mean.[10]

Extension to multi-class classification

The F-score is also used for evaluating classification problems with more than two classes (Multiclass classification). In this setup, the final score is obtained by micro-averaging (biased by class frequency) or macro-averaging (taking all classes as equally important). For macro-averaging, two different formulas have been used by applicants: the F-score of (arithmetic) class-wise precision and recall means or the arithmetic mean of class-wise F-scores, where the latter exhibits more desirable properties.[11]

See also

• Confusion matrix
• METEOR
• BLEU
• NIST (metric)
• Receiver operating characteristic
• ROUGE (metric)
• Uncertainty coefficient, aka Proficiency
• Word error rate

References

1. Sasaki, Y. (2007). "The truth of the F-measure" (PDF).
2. Van Rijsbergen, C. J. (1979). Information Retrieval (2nd ed.). Butterworth-Heinemann.
3. Beitzel., Steven M. (2006). On Understanding and Classifying Web Queries (Ph.D. thesis). IIT. CiteSeerX 10.1.1.127.634.
4. X. Li; Y.-Y. Wang; A. Acero (July 2008). Learning query intent from regularized click graphs. Proceedings of the 31st SIGIR Conference. doi:10.1145/1390334.1390393. S2CID 8482989.
5. See, e.g., the evaluation of the .
6. Derczynski, L. (2016). Complementarity, F-score, and NLP Evaluation. Proceedings of the International Conference on Language Resources and Evaluation.
7. Hand, David. "A note on using the F-measure for evaluating record linkage algorithms - Dimensions". app.dimensions.ai. doi:10.1007/s11222-017-9746-6. hdl:10044/1/46235. Retrieved 2018-12-08.
8. Chicco D, Jurman G (January 2020). "The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation". BMC Genomics. 21 (6): 6. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
9. Powers, David M W (2011). "Evaluation: From Precision, Recall and F-Score to ROC, Informedness, Markedness & Correlation". Journal of Machine Learning Technologies. 2 (1): 37–63. hdl:2328/27165.
10. Tharwat A (August 2018). "Classification assessment methods". Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003.
11. J. Opitz; S. Burst (2019). "Macro F1 and Macro F1". arXiv:1911.03347 [stat.ML].