Ellingham diagram

An Ellingham diagram is a graph showing the temperature dependence of the stability of compounds. This analysis is usually used to evaluate the ease of reduction of metal oxides and sulfides. These diagrams were first constructed by Harold Ellingham in 1944.[1] In metallurgy, the Ellingham diagram is used to predict the equilibrium temperature between a metal, its oxide, and oxygen — and by extension, reactions of a metal with sulfur, nitrogen, and other non-metals. The diagrams are useful in predicting the conditions under which an ore will be reduced to its metal. The analysis is thermodynamic in nature and ignores reaction kinetics. Thus, processes that are predicted to be favourable by the Ellingham diagram can still be slow.

Thermodynamics
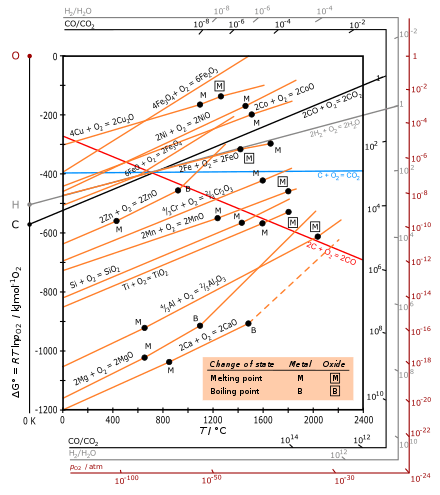
Ellingham diagram for several metals giving the free energy of formation of metal oxides and the corresponding oxygen partial pressure at equilibrium.

Ellingham diagrams are a particular graphical form of the principle that the thermodynamic feasibility of a reaction depends on the sign of ΔG, the Gibbs free energy change, which is equal to ΔH − TΔS, where ΔH is the enthalpy change and ΔS is the entropy change.

The Ellingham diagram plots the Gibbs free energy change (ΔG) for each oxidation reaction as a function of temperature. For comparison of different reactions, all values of ΔG refer to the reaction of the same quantity of oxygen, chosen as one mole O (​1⁄2 mol O
2) by some authors[2] and one mole O
2 by others.[3] The diagram shown refers to 1 mole O
2, so that for example the line for the oxidation of chromium shows ΔG for the reaction ​4⁄3 Cr(s) + O
2(g) → ​2⁄3 Cr
2O
3(s), which is ​2⁄3 of the molar Gibbs energy of formation ΔGf°(Cr
2O
3, s).

In the temperature ranges commonly used, the metal and the oxide are in a condensed state (solid or liquid), and oxygen is a gas with a much larger molar entropy. For the oxidation of each metal, the dominant contribution to the entropy change (ΔS) is the removal of ​1⁄2 mol O
2, so that ΔS is negative and roughly equal for all metals. The slope of the plots [2] is therefore positive for all metals, with ΔG always becoming more negative with lower temperature, and the lines for all the metal oxides are approximately parallel. Since these reactions are exothermic, they always become feasible at lower temperatures. At a sufficiently high temperature, the sign of ΔG may invert (becoming positive) and the oxide can spontaneously reduce to the metal, as shown for Ag and Cu.

For oxidation of carbon, the red line is for the formation of CO: C(s) + ​1⁄2 O
2(g) → CO(g) with an increase in the number of moles of gas, leading to a positive ΔS and a negative slope. The blue line for the formation of CO
2 is approximately horizontal, since the reaction C(s) + O
2(g) → CO
2(g) leaves the number of moles of gas unchanged so that ΔS is small.

As with any chemical reaction prediction based on purely thermodynamic grounds, a spontaneous reaction may be very slow if one or more stages in the reaction pathway have very high activation energies EA.

If two metals are present, two equilibria have to be considered. The oxide with the more negative ΔG will be formed and the other oxide will be reduced.

Diagram features
  1. Curves in the Ellingham diagrams for the formation of metallic oxides are basically straight lines with a positive slope. The slope is proportional to ΔS, which is fairly constant with temperature.
  2. The lower the position of a metal's line in the Ellingham diagram, the greater is the stability of its oxide. For example, the line for Al (oxidation of aluminium) is found to be below that for Fe (formation of Fe
    2    O
    3    ).
  3. Stability of metallic oxides decreases with increase in temperature. Highly unstable oxides like Ag
    2    O     and HgO easily undergo thermal decomposition.
  4. The formation free energy of carbon dioxide (CO
    2    ) is almost independent of temperature, while that of carbon monoxide (CO) has negative slope and crosses the CO
    2     line near 700 °C. According to the Boudouard reaction, carbon monoxide is the dominant oxide of carbon at higher temperatures (above about 700 °C), and the higher the temperature (above 700 °C) the more effective a reductant (reducing agent) carbon is.
  5. If the curves for two metals at a given temperature are compared, the metal with the lower Gibbs free energy of oxidation on the diagram will reduce the oxide with the higher Gibbs free energy of formation. For example, metallic aluminium can reduce iron oxide to metallic iron, the aluminium itself being oxidized to aluminium oxide. (This reaction is employed in thermite.)
  6. The greater the gap between any two lines, the greater the effectiveness of the reducing agent corresponding to the lower line.
  7. The intersection of two lines implies an oxidation-reduction equilibrium. Reduction using a given reductant is possible at temperatures above the intersection point where the ΔG line of that reductant is lower on the diagram than that of the metallic oxide to be reduced. At the point of intersection the free energy change for the reaction is zero, below this temperature it is positive and the metallic oxide is stable in the presence of the reductant, while above the point of intersection the Gibbs energy is negative and the oxide can be reduced.

Reducing agents

In industrial processes, the reduction of metal oxides is often effected by a carbothermic reaction, using carbon as a reducing agent. Carbon is available cheaply as coal, which can be rendered to coke. When carbon reacts with oxygen it forms the gaseous oxides carbon monoxide and carbon dioxide, so the thermodynamics of its oxidation is different from that for metals: its oxidation has a more negative ΔG with higher temperatures (above 700 °C). Carbon can thus serve as reducing agent. Using this property, reduction of metals may be performed as a double redox reaction at relatively low temperature.

Use of Ellingham diagrams

The main application of Ellingham diagrams is in the extractive metallurgy industry, where it helps to select the best reducing agent for various ores in the extraction process, purification and grade setting for steel manufacturing. It also helps to guide the purification of metals, especially the removal of trace elements. The direct reduction process for making iron rests firmly on the guidance of Ellingham diagrams, which show that hydrogen can alone reduce iron oxides to the metal.

Reducing agent for haematite

In iron ore smelting, haematite gets reduced at the top of the furnace, where temperature is in the range 600 – 700 °C. The Ellingham diagram indicates that in this range carbon monoxide acts as a stronger reducing agent than carbon since the process

2 CO + O
2 → 2 CO
2

has a more-negative free energy change than the process:

2 C + O
2 → 2 CO.

In the upper part of the blast furnace, haematite is reduced by CO (produced by oxidation of coke lower down, at higher temperatures) even in the presence of carbon – though this is mainly because the kinetics for gaseous CO reacting with the ore are better.

Reducing agent for chromic oxide-carbon cannot be used

The Ellingham curve for the reaction 2C(s) + O
2(g) → 2CO(g) slopes down and falls below the curves for all the metals. Hence, carbon can normally act as a reducing agent for all metal oxides at very high temperatures. But chromium formed at these temperatures reacts with carbon to form its carbide, which gives undesirable properties to the chromium metal obtained. Hence, for high temperature reduction of chromic oxide, carbon cannot be used.

Alumino thermic process
Thermite reaction proceeding for a railway welding. Shortly after this, the liquid iron flows into the mould around the rail gap

The Ellingham curve for aluminium lies below the curves of most metals such as chromium, iron, etc. This fact indicates that aluminium can be used as the reducing agent for oxides of all these metals. This result is illustrated as follows:

The free energies of formation of chromium(III) oxide and aluminium oxide per mole of oxygen consumed are -541 kJ and -827 kJ respectively. The processes are:

 

 

 

 

(1)

 

 

 

 

(2)

The second equation minus the first equation gives:

 

 

 

 

(3)

So aluminium oxide is more stable than chromium oxide (at least at normal temperatures, and in fact all the way up to the decomposition temperatures of the oxides). Since the Gibbs free energy change is negative, aluminium can reduce chromium oxide.

In pyrometallurgy, aluminium is used as a reducing agent in the alumino-thermic process or thermite process to extract chromium and manganese by reduction of their oxides.

Extensions to other gas-phase reactions

The concept of plotting the free energies of reaction of various elements with a given gas-phase reactant may be extended beyond oxidation reactions. The original paper by Ellingham explicitly to the reduction of both oxygen and sulfur by metallurgical processes,[1] and anticipated the use of such diagrams for other compounds, including chlorides, carbides, and sulfates. The concept is generally useful for studying the comparative stability of compounds across a range of partial pressures and temperatures. The construction of an Ellingham diagram is especially useful when studying the stability of compounds in the presence of a reductant. Ellingham diagrams are now available for bromides, chlorides, fluorides, hydrides, iodides, nitrides, oxides, sulfides, selenides, and tellurides.

gollark: Certainly!
gollark: People are literally dying for stupid reasons. It's not utopian.
gollark: ?????
gollark: If you can make superintelligent and aligned AI, you can do so, so much better.
gollark: https://www.reddit.com/r/rational/comments/e53l5k/dc_ff_scythe_parody/

References
  1. Ellingham, H. J. T. (1944), "Reducibility of oxides and sulphides in metallurgical processes", J. Soc. Chem. Ind. (London), 63 (5): 125, doi:10.1002/jctb.5000630501.
  2. Atkins, Peter; de Paula, Julio (2006), Physical Chemistry: Thermodynamics And Kinetics (8th ed.), W.H. Freeman, p. 215, ISBN 0716785676. This reference plots the diagram upside-down, with ΔG° decreasing upwards.
  3. Ellingham diagram tutorial and interactive diagram (University of Cambridge)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.