Dynamic tonality

Dynamic Tonality is a new paradigm for music which generalizes the special relationship between Just Intonation and the Harmonic Series to apply to a much wider set of pseudo-Just tunings and pseudo-Harmonic timbres. [1] Dynamic Tonality enables many new musical effects that could expand the frontiers of tonality,[2] including polyphonic tuning bends, tuning modulations, new chord progressions, temperament modulations and progressions, and novel timbre effects such as dynamic changes to primeness, conicality, and richness.[3]

The Static Timbre paradigm

Harmonic timbres

A vibrating string, a column or air, and the human voice all emit a specific pattern of partials called the Harmonic Series. ("Partials" are also called "harmonics" and/or "overtones.") Each musical instrument's unique sound is called its timbre, so we can call an instrument's timbre a "Harmonic timbre" if its partials are emitted as per the Harmonic Series.

Just tunings

Just Intonation is a system of tuning that adjusts a tuning's notes to maximize their alignment with a Harmonic timbre's partials. This alignment maximizes the consonance of music's tonal intervals, and is, arguably, the source of tonality.

Temperament

Unfortunately, the Harmonic Series and Just Intonation share an infinitely-complex—i.e., rank-∞—pattern that is determined by the infinite series of prime numbers. A temperament is an attempt to reduce this complexity by mapping this rank-∞ pattern to a simpler—i.e., lower rank—pattern.

Throughout history, the pattern of notes in a tuning could be altered by humans but the pattern of partials sounded by an acoustic musical instrument was unalterably determined by the physics of the Harmonic Series. The resulting misalignment between pseudo-Just tempered tunings and fully-Harmonic untempered timbres made temperament "a battleground for the great minds of Western civilization."[4][5][6] This misalignment, in any tuning that is not fully Just (and hence infinitely complex), is the defining characteristic of the Static Timbre Paradigm.

Instruments

Many of the pseudo-Just temperaments proposed during this "temperament battle" were rank-2 (two-dimensional)—such as quarter-comma meantone—that provided more than 12 notes per octave. However, the standard piano-like keyboard is only rank-1 (one-dimensional), affording at most 12 notes per octave. Piano-like keyboards affording more than 12 notes per octave were developed by Vicentino,[4]:127 Colonna,[4]:131 Mersenne,[4]:181 Huygens,[4]:185 and Newton,[4]:196 but were deemed cumbersome and difficult to learn.[4]:18

The Dynamic Tonality paradigm

The defining characteristic of Dynamic Tonality is that a given rank-2 temperament (as defined by a period α, a generator β, and a comma sequence)[7] is used to generate, in real time during performance, the same set of intervals[1] among:

  1. A pseudo-Just tuning's notes;
  2. A pseudo-Harmonic timbre's partials; and
  3. An isomorphic keyboard's note-controlling buttons.

Generating all three from the same temperament solves two problems and creates (at least) three opportunities.

  1. Dynamic Tonality solves the problem[4][5][6] of maximizing the consonance[8] of tempered tunings, and extends that solution across a much wider range of tunings than were previously considered to be consonant.[7][1]
  2. Dynamic Tonality solves the "cumbersome" problem cited by Isacoff[4]:18,104,196 by generating a keyboard that is (a) isomorphic with its temperament[7] (in every octave, key, and tuning), and yet is (b) tiny (the size of the keyboards on squeezeboxes such as concertinas, bandoneons, and bayans). The creators of Dynamic Tonality could find no evidence that any of Isacoff's Great Minds knew about isomorphic keyboards or recognized the connection between the rank of a temperament and the dimensions of a keyboard (as described in Milne et al. 2007).[7]
  3. Dynamic Tonality gives musicians the opportunity to explore new musical effects (see "New musical effects," below).
  4. Dynamic Tonality creates the opportunity for musicians to explore rank-2 temperaments other than the syntonic temperament (such as schismatic, Magic, and miracle) easily and with maximum consonance.
  5. Dynamic Tonality creates the opportunity for a significant increase in the efficiency of music education.[9]

A rank-2 temperament defines a rank-2 (i.e., two-dimensional) note-space, as shown in Video 1 (Note-space).

The syntonic temperament is a rank-2 temperament defined by its period (just perfect octave, 1/2), its generator (just perfect fifth, 3/2) and its comma sequence (which starts with the syntonic comma, 81/80, which names the temperament). The construction of the syntonic temperament's note-space is shown in Video 2 (Syntonic note-space).

The valid tuning range of the syntonic temperament is show in Figure 1.

Figure 1: The valid tuning range of the syntonic temperament, noting its valid tuning ranges at different p-limits and some notable tunings within those ranges.

A keyboard that is generated by a temperament is said to be isomorphic with that temperament (from the Greek "iso" meaning "same," and "morph" meaning "shape"). Isomorphic keyboards are also known as generalized keyboards. Isomorphic keyboards have the unique properties of transpositional invariance[10] and tuning invariance[7]:4 when used with rank-2 temperaments of just intonation. That is, such keyboards expose a given musical interval with "the same shape" in every octave of every key of every tuning of such a temperament.

Of the various isomorphic keyboards now known (e.g., the Bosanquet, Janko, Fokker, and Wesley), the Wicki-Hayden keyboard is optimal for dynamic tonality across the entire valid 5-limit tuning range of the syntonic temperament.[1]:7-10 The isomorphic keyboard shown in this article's videos is the Wicki-Hayden keyboard, for that reason. It also has symmetries related to Diatonic Set Theory, as shown in Video 3 (Same shape).

The Wicki-Hayden keyboard embodies a tonnetz, as shown in Video 4 (Tonnetz). The tonnetz is a lattice diagram representing tonal space first described by Leonhard Euler in 1739,[11] which is a central feature of Neo-Riemannian music theory.

Non-Western tunings

The endpoints of the valid 5-limit tuning range of the syntonic temperament, shown in Figure 1, are:

  • P5=686 (7-TET): The minor second is as wide as the major second, so the diatonic scale is a seven-note whole tone scale. This is the traditional tuning of the traditional Thai ranat ek, in which the ranat's inharmonic timbre is maximally consonant.[8]:303 Other non-Western musical cultures are also reported to tune their instruments in 7-TET, including the Mandinka balafon.[12]
  • P5=720 (5-TET): The minor second has zero width, so the diatonic scale is a five-note whole tone scale. This is arguably the slendro scale of Java's gamelan orchestras, with which the gamelan's inharmonic timbres are maximally consonant.[8]:73

Dynamic timbres

The partials of a pseudo-Harmonic timbre are digitally mapped, as defined by a temperament, to specific notes of a pseudo-Just tuning. When the temperament's generator changes in width, the tuning of the temperament's notes changes, and the partials change along with those notes—yet their relative position remains invariant on the temperament-generated isomorphic keyboard. The frequencies of notes and partials change with the generator's width, but the relationships among the notes, partials, and note-controlling buttons remain the same: as defined by the temperament. The mapping of partials to the notes of the syntonic temperament is animated in Video 5.

Dynamic tuning

On an isomorphic keyboard, any given musical structure—a scale, a chord, a chord progression, or an entire song—has exactly the same fingering in every tuning of a given temperament. This allows a performer to learn to play a song in one tuning of a given temperament and then to play it with exactly the same finger-movements, on exactly the same note-controlling buttons, in every other tuning of that temperament. See Video 3 (Same Shape).

For example, one could learn to play Rodgers and Hammerstein's Do-Re-Mi in its original 12-tone equal temperament (12-tet) and then play it with exactly the same finger-movements, on exactly the same note-controlling buttons, while smoothly changing the tuning in real time across the syntonic temperament's tuning continuum.

The process of digitally tempering a pseudo-Harmonic timbre's partials to align with a tempered pseudo-Just tuning's notes is shown in Video 6 (Dynamic tuning & timbre).[13]

New musical effects

Dynamic Tonality enables two new kinds of real-time musical effects: those that require a change in tuning, and those that affect the distribution of energy among a pseudo-Harmonic timbre's partials.

Tuning-based effects

Dynamic Tonality's novel tuning-based effects[2] include:

  • Polyphonic tuning bends, in which the pitch of the tonic remains fixed while the pitches of all other notes change to reflect changes in the tuning, with notes that are close to the tonic in tonal space changing pitch only slightly and those that are distant changing considerably;
  • New chord progressions that start in a first tuning, change to second tuning (to progress across a comma which the second tuning tempers out but the first tuning does not), optionally change to subsequent tunings for similar reasons, and then conclude in the first tuning; and
  • Temperament modulations, which start in a first tuning of a first temperament, change to a second tuning of the first temperament which is also a first tuning of a second temperament (a "pivot tuning"), change note-selection among enharmonics to reflect the second temperament, change to a second tuning of the second temperament, then optionally change to additional tunings and temperaments before returning through the pivot tuning to the first tuning of the first temperament.

Timbre-based effects

Dynamic Tonality's novel timbre effects[3]:39-40 include:

  • Primeness: Partials 2, 4, 8, 16, …, 2n are factorised only by prime 2, and so these partials can be said to embody twoness. Partials 3, 9, 27, …, 3n are factorised only by prime 3, and so can be said to embody threeness. Partials 5, 25, 125, …, 5n are factorised only by prime 5, and so can be said to embody fiveness. Other partials are factorised by two, or more, different primes. Partials 12 is factorised by both 2 and 3, and so embodies both twoness and threeness; partial 15 is factorised by 3 and 5, and so embodies both threeness and fiveness. Primeness empowers the musician to manipulate any given timbre such that its twoness, threeness, fiveness, …, primeness can be enhanced or reduced. Adding a second comma to the syntonic temperament's comma sequence defines the 7th partial (see Video 5), thus similarly enabling sevenness.
  • Conicality: Turning down twoness will lead to an odd-partial-only timbre – a “hollow or nasal” sound[14] reminiscent of cylindrical closed bore instruments (e.g. clarinet). As the twoness is turned up, the even partials are gradually introduced creating a sound more reminiscent of open cylindrical bore instruments (e.g. flute, shakuhachi), or conical bore instruments (e.g. bassoon, oboe, saxophone). This perceptual feature is called conicality.
  • Richness: When richness is at minimum, only the fundamental sounds; as it is increased, the twoness gain is increased, then the threeness gain, then the fiveness gain, etc..

Blue notes

The 7th partial is cited by some[15][16] as being the essence of the "blue notes" played in the blues and related music.

Adding the starling comma to the syntonic temperament's comma sequence maps the 7th partial to the fundamental's augmented sixth (see Video 5). On the one hand, adding this narrows the valid tuning range of the syntonic temperament to the 7-limit range of a mere 5 cents (centered on 1/4-comma meantone, P5=696.58 cents; see Figure 1). On the other hand, it adds the 7th partial to the timbre, on a unique note, which gives musicians the option of emphasizing that partial when playing blues-inspired music. (See Primeness above. Real-time changes to the sevenness of a 7-limit timbre could prove to be musically useful.)

The augmented sixth is far to the right of the fundamental on the Wicki-Hayden keyboard (as shown in Video 5), so it is suitable for use in the I-IV-V blues progression in only C and keys flat-ward thereof.

Superset of static timbre paradigm

One can use Dynamic Tonality to temper only the tuning of notes, without tempering timbres, thus embracing the Static Timbre Paradigm.

Similarly, using a synthesizer control such as the Tone Diamond,[17] a musician can opt to maximize regularity, harmonicity, or consonance—or trade off among them in real time (with some of the jammer's 10 degrees of freedom mapped to the Tone Diamond's variables), with consistent fingering. This enables musicians to choose tunings that are regular or irregular, equal or non-equal, major-biased or minor-biased—and enables the musician to slide smoothly among these tuning options in real time, exploring the emotional affect of each variation and the changes among them. Everything that the Static Timbre Paradigm offered, Dynamic Tonality can do—and more.

Compared to microtonality

Imagine that the valid tuning range of a temperament (as defined in Dynamic Tonality) is a string, and that individual tunings are beads on that string. The microtonal community has typically focused primarily on the beads, whereas Dynamic Tonality is focused primarily on the string. Both communities care about both beads and strings; only their focus and emphasis differ.

Example: C2ShiningC

An early example of Dynamic Tonality can be heard in "C to Shining C" C2ShiningC (composed and recorded by William Sethares in April 2008). This sound example contains only one chord, Dmaj (the piece is, oddly enough, recorded or transposed in the recording to D major, despite its name), played throughout, yet a sense of harmonic tension is imparted by a tuning progression and a timbre progression, as follows:

Cmaj 19-tet/harmonic -> Cmaj 5-tet/harmonic -> Cmaj 19-tet/consonant -> Cmaj 5-tet/consonant

  • The timbre progresses from a harmonic timbre (with partials following the harmonic series) to a 'pseudo-harmonic' timbre (with partials adjusted to align with the notes of the current tuning) and back again.
  • Twice as rapidly, the tuning progresses (via polyphonic tuning bends), within the syntonic temperament, from an initial tuning in which the tempered perfect fifth (P5) is 695 cents wide (19-tone equal temperament, 19-tet) to a second tuning in which the P5 is 720 cents wide (5-tet), and back again.

As the tuning changes, the pitches of all notes except the tonic change, and the widths of all intervals except the octave change; however, the relationships among the intervals (as defined by the syntonic temperament's period, generator, and comma sequence) remain invariant (i.e., consistent) throughout. This invariance among a temperament's interval relationships is what makes Dynamic Tonality possible.

In the syntonic temperament, the tempered major third (M3) is as wide as four tempered perfect fifths (P5's) minus two octaves—so the M3's width changes across the tuning progression

  • from 380 cents in 19-tet (P5 = 695), where the Cmaj triad's M3 is very close in width to its just width of 386.3 cents,
  • to 480 cents in 5-tet (P5 = 720), where the Cmaj triad's M3 is close in width to a slightly flat perfect fourth of 498 cents, making the Cmaj chord sound rather like a Csus4.

Thus, the tuning progression's widening of the Cmaj's M3 from a nearly-just major third in 19-tet to a slightly flat perfect fourth in 5-tet creates harmonic tension, which is relieved by the return to 19-tet.

This is an example of Dynamic Tonality's ability to expand the frontiers of tonality by offering new means of creating tension and release, even within a single chord.

History

Dynamic Tonality was developed primarily by a collaboration between Prof. William Sethares, Dr. Andrew Milne, and James "Jim" Plamondon (see papers cited below).

In late 2003, Plamondon was studying the economic forces that compelled the emergence of the QWERTY keyboard standard, which led him to study concertina note-layouts as a possible counter-example. That exposed him to the Wicki-Hayden note-layout. He reached out to dozens of academics in music theory asking "what deep property of music is exposed by this keyboard's invariant note-pattern?", but only Sethares and Milne dug into the problem, applying their knowledge of music and mathematics to publish a series of papers that solved the mystery.[3][7][1] Sethares' previous work, showing that consonance arose solely from the alignment of notes and partials, was a key input to Dynamic Tonality. Milne & Sethares' grad students did much of the work in developing electronic synthesizers and sequencers for Dynamic Tonality.[13]

A prototype of the Thummer.

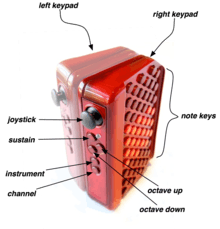
Meanwhile, Plamondon formed Thumtronics Pty Ltd to develop an expressive, tiny, electronic Wicki-Hayden keyboard instrument: Thumtronics' "Thummer." However, he spent too much of the company's limited capital on researching motion-sensing (which is now available in a single-chip solution) and polyphonic aftertouch, so the company failed before it could bring the Thummer to market. The generic name for a Thummer-like instrument is "jammer." With two thumb-sticks and internal motion sensors, a jammer would afford 10 degrees of freedom, which would make it the most expressive polyphonic instrument available. Without the expressive potential of a jammer, musicians lack the expressive power needed to exploit Dynamic Tonality in real time, so Dynamic Tonality's new tonal frontiers remain largely unexplored.

Musica Facta

Dynamic Tonality is the foundation of a broad research project named Musica Facta—meaning created music—that unites a loose association of collaborators in their explorations of Dynamic Tonality's invariances, isomorphisms, and the implications thereof.

gollark: ++magic reload_ext irc_link
gollark: Test.
gollark: ÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆÆ
gollark: ++magic reload_ext telephone
gollark: BeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBeesBe
  • DynamicTonality.com, where you can find music-creation tools that are compatible with Dynamic Tonality.

References
  1. Milne, Andrew; Sethares, William; Plamondon, James (29 Aug 2008). "Tuning Continua and Keyboard Layouts". Journal of Mathematics and Music. 2 (1): 1–19. doi:10.1080/17459730701828677. Archived from the original on 5 August 2012. Retrieved 11 May 2020. Alt URL
  2. Plamondon, Jim; Milne, Andrew J.; Sethares, William (2009). Dynamic Tonality: Extending the Framework of Tonality into the 21st Century (PDF). Proceedings of the Annual Conference of the South Central Chapter of the College Music Society.
  3. Milne, A.; Sethares, W.; Plamondon, J. (2006). "X System" (PDF). Technical Report, Thumtronics Inc. Retrieved 2020-05-02. The definitions of primeness, conicality, and richness were copied from this source, which is available under a Creative Commons Attribution-ShareAlike 3.0 Unported license and the GNU Free Documentation License.
  4. Isacoff, Stuart (2003). Temperament: How Music Became a Battleground for the Great Minds of Western Civilization. Knopf. ISBN 978-0375403552.
  5. Barbour, J.M., 2004, Tuning and Temperament: A Historical Survey
  6. Duffin, R.W., 2006, How Equal Temperament Ruined Harmony (and Why You Should Care)
  7. Milne, A.; Sethares, W.A.; Plamondon, J. (Winter 2007). "Invariant Fingerings Across a Tuning Continuum". Computer Music Journal. 31 (4): 15–32. doi:10.1162/comj.2007.31.4.15. Archived from the original on 1 June 2018. Retrieved 11 May 2020. Alt URL
  8. Sethares, W.A. (2004). Tuning, Timbre, Spectrum, Scale. Springer. ISBN 978-1852337971.
  9. Plamondon, Jim; Milne, Andrew J.; Sethares, William (2009). "Sight-reading music theory: A thought experiment on improving pedagogical efficiency". Technical report, Thumtronics Pty Ltd. Retrieved 11 May 2020.
  10. Keislar, D., History and Principles of Microtonal Keyboard Design, Report No. STAN-M-45, Center for Computer Research in Music and Acoustics, Stanford University, April 1988.
  11. Euler, Leonhard (1739). Tentamen novae theoriae musicae ex certissismis harmoniae principiis dilucide expositae (in Latin). Saint Petersburg Academy. p. 147.
  12. Jessup, L. (1983). The Mandinka Balafon: An Introduction with Notation for Teaching. Xylo Publications.
  13. Sethares, William; Milne, A.; Tiedje, S.; Prechtl, A.; Plamondon, J. (2009). "Spectral Tools for Dynamic Tonality and Audio Morphing". Computer Music Journal. 33 (2): 71–84. doi:10.1162/comj.2009.33.2.71. Retrieved 2009-09-20.
  14. von Helmholtz, Hermann (1885). On the sensations of tone as a physiological basis for the theory of music. Translated by Ellis, Alexander J. (Second English ed.). London: Longmans, Green, and Co. p. 52. Retrieved 2020-05-13.
  15. Mathieu, Allaudin (1997). Harmonic Experience: Tonal Harmony from Its Natural Origins to Its Modern Expression. University Press of Mississippi. ISBN 978-0892815609.
  16. Kubik, Gerhard (1999). Africa and the Blues. University Press of Mississippi. p. 183. ISBN 978-1578061464.
  17. Milne, A., The Tone Diamond, Technical report, The MARCS Institute for Brain, Behaviour and Development, University of Western Sydney, April 2002.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.