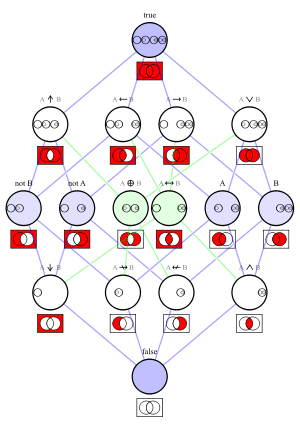
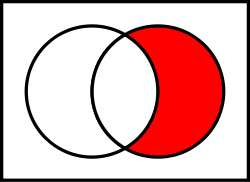
Converse nonimplication

In logic, converse nonimplication[1] is a logical connective which is the negation of converse implication (equivalently, the negation of the converse of implication).

Venn diagram of ${\displaystyle P\nleftarrow Q}$
(the red area is true)

Definition

Converse nonimplication is notated ${\displaystyle P\nleftarrow Q}$, or ${\displaystyle P\not \subset Q}$, and is logically equivalent to ${\displaystyle \neg (P\leftarrow Q)}$

Truth table

The truth table of ${\displaystyle P\nleftarrow Q}$.[2]

${\displaystyle P}$	${\displaystyle Q}$	${\displaystyle P\nleftarrow Q}$
T	T	F
T	F	F
F	T	T
F	F	F

Notation

Converse nonimplication is notated ${\displaystyle \textstyle {p\nleftarrow q}}$, which is the left arrow from converse implication (${\displaystyle \textstyle {\leftarrow }}$), negated with a stroke (/).

Alternatives include

• ${\displaystyle \textstyle {p\not \subset q}}$, which combines converse implication's ${\displaystyle \subset }$, negated with a stroke (/).
• ${\displaystyle \textstyle {p{\tilde {\leftarrow }}q}}$, which combines converse implication's left arrow(${\displaystyle \textstyle {\leftarrow }}$) with negation's tilde(${\displaystyle \textstyle {\sim }}$).
• Mpq, in Bocheński notation

Properties

falsehood-preserving: The interpretation under which all variables are assigned a truth value of 'false' produces a truth value of 'false' as a result of converse nonimplication

Natural language

Grammatical

"p from q."

Classic passive aggressive: "yeah, no"

Rhetorical

"not A but B"

Colloquial

Boolean algebra

Converse Nonimplication in a general Boolean algebra is defined as ${\textstyle {q\nleftarrow p=q'p}\!}$.

Example of a 2-element Boolean algebra: the 2 elements {0,1} with 0 as zero and 1 as unity element, operators ${\textstyle \sim }$ as complement operator, ${\textstyle \vee }$ as join operator and ${\textstyle \wedge }$ as meet operator, build the Boolean algebra of propositional logic.

${\textstyle {}\sim x}$ 1 0 x 0 1	and	y 1 1 1 0 0 1 ${\textstyle y_{\vee }x}$ 0 1 x	and	y 1 0 1 0 0 0 ${\textstyle y_{\wedge }x}$ 0 1 x	then ${\displaystyle \scriptstyle {y\nleftarrow x}\!}$ means	y 1 0 0 0 0 1 ${\displaystyle \scriptstyle {y\nleftarrow x}\!}$ 0 1 x
(Negation)		(Inclusive or)		(And)		(Converse nonimplication)

Example of a 4-element Boolean algebra: the 4 divisors {1,2,3,6} of 6 with 1 as zero and 6 as unity element, operators ${\displaystyle \scriptstyle {^{c}}\!}$ (codivisor of 6) as complement operator, ${\displaystyle \scriptstyle {_{\vee }}\!}$ (least common multiple) as join operator and ${\displaystyle \scriptstyle {_{\wedge }}\!}$ (greatest common divisor) as meet operator, build a Boolean algebra.

${\displaystyle \scriptstyle {x^{c}}\!}$ 6 3 2 1 x 1 2 3 6	and	y 6 6 6 6 6 3 3 6 3 6 2 2 2 6 6 1 1 2 3 6 ${\displaystyle \scriptstyle {y_{\vee }x}\!}$ 1 2 3 6 x	and	y 6 1 2 3 6 3 1 1 3 3 2 1 2 1 2 1 1 1 1 1 ${\displaystyle \scriptstyle {y_{\wedge }x}\!}$ 1 2 3 6 x	then ${\displaystyle \scriptstyle {y\nleftarrow x}\!}$ means	y 6 1 1 1 1 3 1 2 1 2 2 1 1 3 3 1 1 2 3 6 ${\displaystyle \scriptstyle {y\nleftarrow x}\!}$ 1 2 3 6 x
(Codivisor 6)		(Least common multiple)		(Greatest common divisor)		(x's greatest divisor coprime with y)

Properties

Non-associative

${\displaystyle \scriptstyle {r\nleftarrow (q\nleftarrow p)=(r\nleftarrow q)\nleftarrow p}}$ iff ${\displaystyle \scriptstyle {rp=0}}$ #s5 (In a two-element Boolean algebra the latter condition is reduced to ${\displaystyle \scriptstyle {r=0}}$ or ${\displaystyle \scriptstyle {p=0}}$). Hence in a nontrivial Boolean algebra Converse Nonimplication is nonassociative.

${\displaystyle {\begin{aligned}(r\nleftarrow q)\nleftarrow p&=r'q\nleftarrow p&{\text{(by definition)}}\\&=(r'q)'p&{\text{(by definition)}}\\&=(r+q')p&{\text{(De Morgan's laws)}}\\&=(r+r'q')p&{\text{(Absorption law)}}\\&=rp+r'q'p\\&=rp+r'(q\nleftarrow p)&{\text{(by definition)}}\\&=rp+r\nleftarrow (q\nleftarrow p)&{\text{(by definition)}}\\\end{aligned}}}$

Clearly, it is associative iff ${\displaystyle \scriptstyle {rp=0}}$.

Non-commutative

• ${\displaystyle \scriptstyle {q\nleftarrow p=p\nleftarrow q\,}\!}$ iff ${\displaystyle \scriptstyle {q=p\,}\!}$ #s6. Hence Converse Nonimplication is noncommutative.

Neutral and absorbing elements

• 0 is a left neutral element (${\displaystyle \scriptstyle {0\nleftarrow p=p}\!}$) and a right absorbing element (${\displaystyle \scriptstyle {p\nleftarrow 0=0}\!}$).
• ${\displaystyle \scriptstyle {1\nleftarrow p=0}\!}$, ${\displaystyle \scriptstyle {p\nleftarrow 1=p'}\!}$, and ${\displaystyle \scriptstyle {p\nleftarrow p=0}\!}$.
• Implication ${\displaystyle \scriptstyle {q\rightarrow p}\!}$ is the dual of converse nonimplication ${\displaystyle \scriptstyle {q\nleftarrow p}\!}$ #s7.

Converse Nonimplication is noncommutative
Step	Make use of	Resulting in
${\displaystyle \scriptstyle \mathrm {s.1} }$	Definition	${\displaystyle \scriptstyle {q{\tilde {\leftarrow }}p=q'p\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.2} }$	Definition	${\displaystyle \scriptstyle {p{\tilde {\leftarrow }}q=p'q\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.3} }$	${\displaystyle \scriptstyle \mathrm {s.1\ s.2} }$	${\displaystyle \scriptstyle {q{\tilde {\leftarrow }}p=p{\tilde {\leftarrow }}q\ \Leftrightarrow \ q'p=qp'\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.4} }$		${\displaystyle \scriptstyle {q\,}\!}$	${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {q.1\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.5} }$	${\displaystyle \scriptstyle \mathrm {s.4.right} }$ - expand Unit element		${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {q.(p+p')\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.6} }$	${\displaystyle \scriptstyle \mathrm {s.5.right} }$ - evaluate expression		${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {qp+qp'\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.7} }$	${\displaystyle \scriptstyle \mathrm {s.4.left=s.6.right} }$	${\displaystyle \scriptstyle {q=qp+qp'\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.8} }$		${\displaystyle \scriptstyle {q'p=qp'\,}\!}$	${\displaystyle \scriptstyle {\Rightarrow \,}\!}$	${\displaystyle \scriptstyle {qp+qp'=qp+q'p\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.9} }$	${\displaystyle \scriptstyle \mathrm {s.8} }$ - regroup common factors		${\displaystyle \scriptstyle {\Rightarrow \,}\!}$	${\displaystyle \scriptstyle {q.(p+p')=(q+q').p\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.10} }$	${\displaystyle \scriptstyle \mathrm {s.9} }$ - join of complements equals unity		${\displaystyle \scriptstyle {\Rightarrow \,}\!}$	${\displaystyle \scriptstyle {q.1=1.p\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.11} }$	${\displaystyle \scriptstyle \mathrm {s.10.right} }$ - evaluate expression		${\displaystyle \scriptstyle {\Rightarrow \,}\!}$	${\displaystyle \scriptstyle {q=p\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.12} }$	${\displaystyle \scriptstyle \mathrm {s.8\ s.11} }$	${\displaystyle \scriptstyle {q'p=qp'\ \Rightarrow \ q=p\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.13} }$		${\displaystyle \scriptstyle {q=p\ \Rightarrow \ q'p=qp'\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.14} }$	${\displaystyle \scriptstyle \mathrm {s.12\ s.13} }$	${\displaystyle \scriptstyle {q=p\ \Leftrightarrow \ q'p=qp'\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.15} }$	${\displaystyle \scriptstyle \mathrm {s.3\ s.14} }$	${\displaystyle \scriptstyle {q{\tilde {\leftarrow }}p=p{\tilde {\leftarrow }}q\ \Leftrightarrow \ q=p\,}\!}$

Implication is the dual of Converse Nonimplication
Step	Make use of	Resulting in
${\displaystyle \scriptstyle \mathrm {s.1} }$	Definition	${\displaystyle \scriptstyle {\operatorname {dual} (q{\tilde {\leftarrow }}p)\,}\!}$	${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {\operatorname {dual} (q'p)\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.2} }$	${\displaystyle \scriptstyle \mathrm {s.1.right} }$ - .'s dual is +		${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {q'+p\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.3} }$	${\displaystyle \scriptstyle \mathrm {s.2.right} }$ - Involution complement		${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {(q'+p)''\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.4} }$	${\displaystyle \scriptstyle \mathrm {s.3.right} }$ - De Morgan's laws applied once		${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {(qp')'\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.5} }$	${\displaystyle \scriptstyle \mathrm {s.4.right} }$ - Commutative law		${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {(p'q)'\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.6} }$	${\displaystyle \scriptstyle \mathrm {s.5.right} }$		${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {(p{\tilde {\leftarrow }}q)'\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.7} }$	${\displaystyle \scriptstyle \mathrm {s.6.right} }$		${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {p\leftarrow q\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.8} }$	${\displaystyle \scriptstyle \mathrm {s.7.right} }$		${\displaystyle \scriptstyle {=\,}\!}$	${\displaystyle \scriptstyle {q\rightarrow p\,}\!}$
${\displaystyle \scriptstyle \mathrm {s.9} }$	${\displaystyle \scriptstyle \mathrm {s.1.left=s.8.right} }$	${\displaystyle \scriptstyle {\operatorname {dual} (q{\tilde {\leftarrow }}p)=q\rightarrow p\,}\!}$

Computer science

An example for converse nonimplication in computer science can be found when performing a right outer join on a set of tables from a database, if records not matching the join-condition from the "left" table are being excluded.[3]

References

1. Lehtonen, Eero, and Poikonen, J.H.
2. Knuth 2011, p. 49
3. http://www.codinghorror.com/blog/2007/10/a-visual-explanation-of-sql-joins.html

• Knuth, Donald E. (2011). The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1 (1st ed.). Addison-Wesley Professional. ISBN 0-201-03804-8.CS1 maint: ref=harv (link)

External links

• Media related to Converse nonimplication at Wikimedia Commons