Conical coordinates

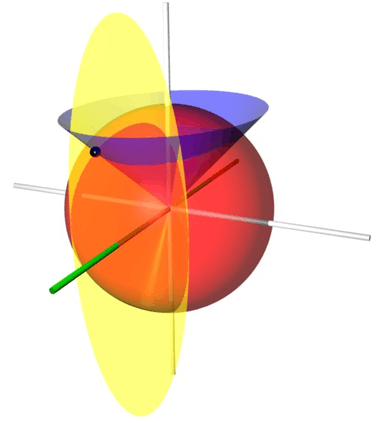
Conical coordinates are a three-dimensional orthogonal coordinate system consisting of concentric spheres (described by their radius r) and by two families of perpendicular cones, aligned along the z- and x-axes, respectively.

Coordinate surfaces of the conical coordinates. The constants b and c were chosen as 1 and 2, respectively. The red sphere represents r = 2, the blue elliptic cone aligned with the vertical z-axis represents μ=cosh(1) and the yellow elliptic cone aligned with the (green) x-axis corresponds to ν² = 2/3. The three surfaces intersect at the point P (shown as a black sphere) with Cartesian coordinates roughly (1.26, -0.78, 1.34). The elliptic cones intersect the sphere in taco-shaped curves.

Basic definitions

The conical coordinates ${\displaystyle (r,\mu ,\nu )}$ are defined by

${\displaystyle x={\frac {r\mu \nu }{bc}}}$

${\displaystyle y={\frac {r}{b}}{\sqrt {\frac {\left(\mu ^{2}-b^{2}\right)\left(\nu ^{2}-b^{2}\right)}{\left(b^{2}-c^{2}\right)}}}}$

${\displaystyle z={\frac {r}{c}}{\sqrt {\frac {\left(\mu ^{2}-c^{2}\right)\left(\nu ^{2}-c^{2}\right)}{\left(c^{2}-b^{2}\right)}}}}$

with the following limitations on the coordinates

${\displaystyle \nu ^{2}<c^{2}<\mu ^{2}<b^{2}.}$

Surfaces of constant r are spheres of that radius centered on the origin

${\displaystyle x^{2}+y^{2}+z^{2}=r^{2},}$

whereas surfaces of constant ${\displaystyle \mu }$ and ${\displaystyle \nu }$ are mutually perpendicular cones

${\displaystyle {\frac {x^{2}}{\mu ^{2}}}+{\frac {y^{2}}{\mu ^{2}-b^{2}}}+{\frac {z^{2}}{\mu ^{2}-c^{2}}}=0}$

and

${\displaystyle {\frac {x^{2}}{\nu ^{2}}}+{\frac {y^{2}}{\nu ^{2}-b^{2}}}+{\frac {z^{2}}{\nu ^{2}-c^{2}}}=0.}$

In this coordinate system, both Laplace's equation and the Helmholtz equation are separable.

Scale factors

The scale factor for the radius r is one (h_r = 1), as in spherical coordinates. The scale factors for the two conical coordinates are

${\displaystyle h_{\mu }=r{\sqrt {\frac {\mu ^{2}-\nu ^{2}}{\left(b^{2}-\mu ^{2}\right)\left(\mu ^{2}-c^{2}\right)}}}}$

and

${\displaystyle h_{\nu }=r{\sqrt {\frac {\mu ^{2}-\nu ^{2}}{\left(b^{2}-\nu ^{2}\right)\left(c^{2}-\nu ^{2}\right)}}}.}$

Light cone conical coordinates

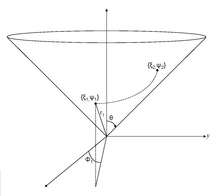
An alternative set of (non-orthogonal) conical coordinates have been derived[1]

${\displaystyle {\begin{aligned}\xi &=r\cos(\phi \sin \theta )\\\psi &=r\sin(\phi \sin \theta )\\\zeta &=\theta ,\end{aligned}}}$

where ${\displaystyle \{r,\theta ,\phi \}}$ are spherical polar coordinates. The corresponding inverse relations are

${\displaystyle {\begin{aligned}r&={\sqrt {\xi ^{2}+\psi ^{2}}}\\\phi &={\frac {1}{\sin \zeta }}\arctan({\frac {\psi }{\xi }})\\\theta &=\zeta .\end{aligned}}}$

The infinitesimal Euclidean distance between two points in these coordinates

${\displaystyle {\begin{aligned}ds^{2}&=d\xi ^{2}+d\psi ^{2}+(\xi ^{2}+\psi ^{2})(1+\arctan({\frac {\psi }{\xi }})^{2}\cot \zeta ^{2})d\zeta ^{2}\\&+2\psi \arctan({\frac {\psi }{\xi }})\cot \zeta d\xi d\zeta -2\xi \arctan({\frac {\psi }{\xi }})\cot \zeta d\psi d\zeta .\end{aligned}}}$

${\displaystyle \xi }$ and ${\displaystyle \psi }$ are orthogonal coordinates on the surface of the cone given by ${\displaystyle \zeta ={\frac {\pi }{4}}}$. If the path between any two points is constrained to this surface, then the geodesic distance between any two points

${\displaystyle \{\xi _{1},\psi _{1},\zeta _{1}={\frac {\pi }{4}}\}}$ and ${\displaystyle \{\xi _{2},\psi _{2},\zeta _{2}={\frac {\pi }{4}}\}}$ is

${\displaystyle s_{12}^{2}=(\xi _{1}-\xi _{2})^{2}+(\psi _{1}-\psi _{2})^{2}.}$

References

1. Drake, Samuel Picton; Anderson, Brian D. O.; Yu, Changbin (2009-07-20). "Causal association of electromagnetic signals using the Cayley–Menger determinant". Applied Physics Letters. 95 (3): 034106. arXiv:0908.3143. Bibcode:2009ApPhL..95c4106D. doi:10.1063/1.3180815. ISSN 0003-6951.

Bibliography

• Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 659. ISBN 0-07-043316-X. LCCN 52011515.
• Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 183–184. LCCN 55010911.
• Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 179. LCCN 59014456. ASIN B0000CKZX7.
• Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. pp. 991–100. LCCN 67025285.
• Arfken G (1970). Mathematical Methods for Physicists (2nd ed.). Orlando, FL: Academic Press. pp. 118–119. ASIN B000MBRNX4.
• Moon P, Spencer DE (1988). "Conical Coordinates (r, θ, λ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 37–40 (Table 1.09). ISBN 978-0-387-18430-2.

External links

• MathWorld description of conical coordinates