Congruent isoscelizers point

In geometry the congruent isoscelizers point is a special point associated with a plane triangle. It is a triangle center and it is listed as X(173) in Clark Kimberling's Encyclopedia of Triangle Centers. This point was introduced to the study of triangle geometry by Peter Yff in 1989.[1][2]

Definition
P1Q1 = P2Q2 = P3Q3

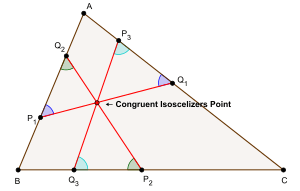
An isoscelizer of an angle A in a triangle ABC is a line through points P1 and Q1, where P1 lies on AB and Q1 on AC, such that the triangle AP1Q1 is an isosceles triangle. An isoscelizer of angle A is a line perpendicular to the bisector of angle A.

Let ABC be any triangle. Let P1Q1, P2Q2, P3Q3 be the isoscelizers of the angles A, B, C respectively such that they all have the same length. Then, for a unique configuration, the three isoscelizers P1Q1, P2Q2, P3Q3 are concurrent. The point of concurrence is the congruent isoscelizers point of triangle ABC.[1]

Properties
Construction for congruent isoscelizers point. A'B'C' is the intouch triangle of triangle ABC and A' 'B' ' C' ' is the intouch triangle of triangle A'B'C' .
( cos ( B/2 ) + cos ( C/2 ) - cos (A/2') : cos ( C/2 ) + cos ( A/2 ) - cos (B/2') : cos ( A/2 ) + cos ( B/2 ) - cos (C/2') )
= ( tan ( A/2 ) + sec ( A/2 ) : tan ( B/2 ) + sec ( B/2 ) : tan ( C/2 ) + sec ( C/2 ) )
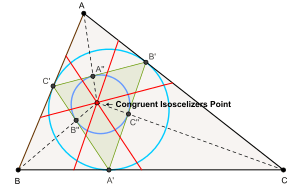
  • The intouch triangle of the intouch triangle of triangle ABC is perspective to triangle ABC, and the congruent isoscelizers point is the perspector. This fact can be used to locate by geometrical constructions the congruent isoscelizers point of any given triangle ABC.[1]
gollark: I'm not sure what "mental state" is supposed to mean, but arguably that's one of the more reasonable things to discriminate based on, given that that's at least partly controlled by the person in question and maybe includes stuff like "being annoying/trolly".
gollark: I don't know how many I'm on, so that's not helpful really.
gollark: Out of the ones I'm on I think three have.
gollark: Not everyone has to. I don't really see the point personally.
gollark: GIFs are just an uncool format.

See also

References
  1. Kimberling, Clark. "X(173) = Congruent isoscelizers point". Encyclopedia of Triangle Centers. Archived from the original on 19 April 2012. Retrieved 3 June 2012.
  2. Kimberling, Clark. "Congruent isoscelizers point". Retrieved 3 June 2012.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.