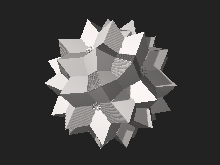Compound of twenty octahedra with rotational freedom

The compound of twenty octahedra with rotational freedom is a uniform polyhedron compound. It's composed of a symmetric arrangement of 20 octahedra, considered as triangular antiprisms. It can be constructed by superimposing two copies of the compound of 10 octahedra UC₁₆, and for each resulting pair of octahedra, rotating each octahedron in the pair by an equal and opposite angle θ.

Compound of twenty octahedra with rotational freedom
Type	Uniform compound
Index	UC13
Polyhedra	20 octahedra
Faces	40+120 triangles
Edges	240
Vertices	120
Symmetry group	icosahedral (Ih)
Subgroup restricting to one constituent	6-fold improper rotation (S6)

When θ is zero or 60 degrees, the octahedra coincide in pairs yielding (two superimposed copies of) the compounds of ten octahedra UC₁₆ and UC₁₅ respectively. When

${\displaystyle \theta =2\tan ^{-1}\left({\sqrt {{\frac {1}{3}}\left(13-4{\sqrt {10}}\right)}}\right)\approx 37.76124^{\circ },}$

octahedra (from distinct rotational axes) coincide in sets four, yielding the compound of five octahedra. When

${\displaystyle \theta =2\tan ^{-1}\left({\frac {-4{\sqrt {3}}-2{\sqrt {15}}+{\sqrt {132+60{\sqrt {5}}}}}{4+{\sqrt {2}}+2{\sqrt {5}}+{\sqrt {10}}}}\right)\approx 14.33033^{\circ },}$

the vertices coincide in pairs, yielding the compound of twenty octahedra (without rotational freedom).

Cartesian coordinates

Cartesian coordinates for the vertices of this compound are all the cyclic permutations of

${\displaystyle {\begin{aligned}&\scriptstyle {\Big (}\pm 2{\sqrt {3}}\sin \theta ,\,\pm (\tau ^{-1}{\sqrt {2}}+2\tau \cos \theta ),\,\pm (\tau {\sqrt {2}}-2\tau ^{-1}\cos \theta ){\Big )}\\&\scriptstyle {\Big (}\pm ({\sqrt {2}}-\tau ^{2}\cos \theta +\tau ^{-1}{\sqrt {3}}\sin \theta ),\,\pm ({\sqrt {2}}+(2\tau -1)\cos \theta +{\sqrt {3}}\sin \theta ),\,\pm ({\sqrt {2}}+\tau ^{-2}\cos \theta -\tau {\sqrt {3}}\sin \theta ){\Big )}\\&\scriptstyle {\Big (}\pm (\tau ^{-1}{\sqrt {2}}-\tau \cos \theta -\tau {\sqrt {3}}\sin \theta ),\,\pm (\tau {\sqrt {2}}+\tau ^{-1}\cos \theta +\tau ^{-1}{\sqrt {3}}\sin \theta ),\,\pm (3\cos \theta -{\sqrt {3}}\sin \theta ){\Big )}\\&\scriptstyle {\Big (}\pm (-\tau ^{-1}{\sqrt {2}}+\tau \cos \theta -\tau {\sqrt {3}}\sin \theta ),\,\pm (\tau {\sqrt {2}}+\tau ^{-1}\cos \theta -\tau ^{-1}{\sqrt {3}}\sin \theta ),\,\pm (3\cos \theta +{\sqrt {3}}\sin \theta ){\Big )}\\&\scriptstyle {\Big (}\pm (-{\sqrt {2}}+\tau ^{2}\cos \theta +\tau ^{-1}{\sqrt {3}}\sin \theta ),\,\pm ({\sqrt {2}}+(2\tau -1)\cos \theta -{\sqrt {3}}\sin \theta ),\,\pm ({\sqrt {2}}+\tau ^{-2}\cos \theta +\tau {\sqrt {3}}\sin \theta ){\Big )}\end{aligned}}}$

where τ = (1 + √5)/2 is the golden ratio (sometimes written φ).

Gallery

• Compounds of twenty octahedra with rotational freedom
• 
  θ = 0°
• 
  θ = 5°
• 
  θ = 10°
• 
  θ = 15°
• 
  θ = 20°
• 
  θ = 25°
• 
  θ = 30°
• 
  θ = 35°
• 
  θ = 40°
• 
  θ = 45°
• 
  θ = 50°
• 
  θ = 55°
• 
  θ = 60°

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.