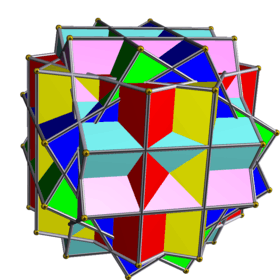
Compound of six cubes with rotational freedom

This uniform polyhedron compound is a symmetric arrangement of 6 cubes, considered as square prisms. It can be constructed by superimposing six identical cubes, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic faces. Each cube is rotated by an equal (and opposite, within a pair) angle θ.

Compound of six cubes with rotational freedom
Type	Uniform compound
Index	UC7
Polyhedra	6 cubes
Faces	12+24 squares
Edges	72
Vertices	48
Symmetry group	octahedral (Oh)
Subgroup restricting to one constituent	4-fold rotational (C4h)

When θ = 0, all six cubes coincide. When θ is 45 degrees, the cubes coincide in pairs yielding (two superimposed copies of) the compound of three cubes.

Cartesian coordinates

Cartesian coordinates for the vertices of this compound are all the permutations of

${\displaystyle (\pm (\cos(\theta )+\sin(\theta )),\pm (\cos(\theta )-\sin(\theta )),\pm 1).}$

Gallery

• Compounds of six cubes with rotational freedom
• 
  θ = 0°
• 
  θ = 5°
• 
  θ = 10°
• 
  θ = 15°
• 
  θ = 20°
• 
  θ = 25°
• 
  θ = 30°
• 
  θ = 35°
• 
  θ = 40°
• 
  θ = 45°

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554.