Compound of three cubes
This uniform polyhedron compound is a symmetric arrangement of 3 cubes, considered as square prisms. It can be constructed by superimposing three identical cubes, and then rotating each by 45 degrees about a separate axis (that passes through the centres of two opposite faces).
| Compound of three cubes | |
|---|---|
 | |
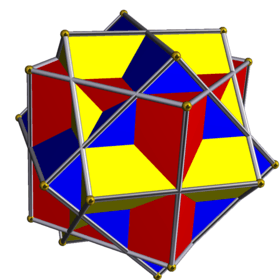| Type | Uniform compound |
| Index | UC8 |
| Convex hull | Nonuniform truncated octahedron |
| Polyhedra | 3 cubes |
| Faces | 6+12 squares |
| Edges | 36 |
| Vertices | 24 |
| Symmetry group | octahedral (Oh) |
| Subgroup restricting to one constituent | 4-fold prismatic (D4h) |
This compound appears in the lithograph print Waterfall by M.C. Escher. Its dual, the compound of three octahedra, forms the central image in an earlier Escher woodcut, Stars.
Cartesian coordinates
Cartesian coordinates for the vertices of this compound are all the permutations of
- (±√2, 0, ±1)
Related compounds
If the cubes are compressed into rhombic prisms, a compound of 3 rhombic prisms is constructed. The compound has pyritohedral symmetry.[1]
Its vertices are parametrized with lengths a and b with values besides √2.
- (±a, 0, ±1), ( 0, ±b, ±1)
- (±b, ±1, 0), ( 0, ±1, ±a)
- (±1, ±a, 0), (±1, 0, ±b)
gollark: And the computer science conspiracies, the mathematics conspiracies, the astronomy conspiracies, the entomology conspiracies, the etymology conspiracies, the rock climbing conspiracies, the nutritionist conspiracies... are we just going to ignore those?
gollark: #karens-corner-of-coronavirus-tales maybe?
gollark: Given the US government's ability to mess up everything it touches, I don't think government-paid government-run healthcare would be the best of ideas. But the insurance system is also quite terrible. There's probably an alternative possibly-better way.
gollark: You can't easily go around controlling spread neatly to just people who accept a 0.5% or whatever risk of death (which is still quite bad).
gollark: That doesn't, in itself, make it bad. It's bad because you're, well, killing someone.
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.