Chip-firing game

The chip-firing game is a one-player game on a graph which was invented around 1983 and since has become an important part of the study of structural combinatorics.

Example graph
A possible firing sequence, with the state variables s(v) in red, and the vertex to be fired in yellow.

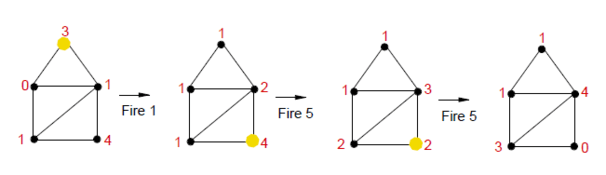
Definition

Let the finite graph G be connected and loopless, with vertices V = {1, 2, . . . , n}. Let deg(v) be the degree of a vertex, and e(v,w) the number of edges between vertices v and w. A configuration or state of the game is defined by assigning each vertex a nonnegative integer s(v), representing the number of chips on this vertex. A move starts with selecting a vertex w which has at least as many chips as its degree: s(w) ≥ deg(w). The vertex w is fired, moving one chip from w along each incident edge to a neighbouring vertex, producing a new configuration defined by:

and for v ≠ w,

A state in which no further firing is possible is a stable state. Starting from an initial configuration, the game proceeds with the following results.

  • If the number of chips is less than the number of edges, the game is always finite, reaching a stable state.
  • If each vertex has fewer chips than its degree, the game is finite.
  • If the number of chips is at least the number of edges, the game can be infinite, never reaching a stable state, for an appropriately chosen initial configuration.
  • If the number of chips is more than twice the number of edges minus the number of vertices, the game is always infinite.

Biggs's Variant

In a variant form of chip-firing closely related to the sandpile model, also known as the dollar game, a single special vertex q is designated as the bank, and is allowed to go into debt, taking a negative integer value s(q) < 0. If any other vertex can fire, the bank cannot fire, only collecting chips. Eventually, q will accumulate so many chips that no other vertex can fire: only in such a state, vertex q can fire chips to neighbouring vertices to "jump start the economy".

The set of states which are stable (i.e. for which only q can fire) and recurrent for this game can be given the structure of an abelian group which is isomorphic to the direct product of and the sandpile group (also referred to as Jacobian group or critical group). The order of the latter is the tree number of the graph.[1][2]

gollark: Testbot2, starch.
gollark: testbot3, take apiomemetics.
gollark: the number of apioforms i have is 1.07% of infinity.
gollark: +>eval markovchains[m.author.id].gen()
gollark: Quarantined bots are in here too, yeß?

See also

References
  1. Biggs, Norman L. (25 June 1997). "Chip-Firing and the Critical Group of a Graph" (PDF). Journal of Algebraic Combinatorics: 25–45. Retrieved 10 May 2014.
  2. wikidot. "Chip-firing references". Retrieved 19 May 2014.
  • A. Björner, L. Lovász, P. W. Shor: Chip-firing games on graphs. European Journal of Combinatorics archive, Volume 12 Issue 4, July 1991, Pages 283–291 doi:10.1016/S0195-6698(13)80111-4 PDF
  • A. Björner, L. Lovász: Chip-Firing Games on Directed Graphs. Journal of Algebraic Combinatorics, December 1992, Volume 1, Issue 4, pp 305–328 doi:10.1023/A:1022467132614
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.