Loop (graph theory)
In graph theory, a loop (also called a self-loop or a "buckle") is an edge that connects a vertex to itself. A simple graph contains no loops.
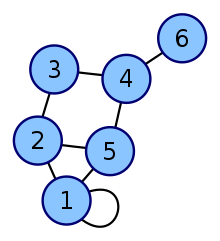
Depending on the context, a graph or a multigraph may be defined so as to either allow or disallow the presence of loops (often in concert with allowing or disallowing multiple edges between the same vertices):
- Where graphs are defined so as to allow loops and multiple edges, a graph without loops or multiple edges is often distinguished from other graphs by calling it a "simple graph".
- Where graphs are defined so as to disallow loops and multiple edges, a graph that does have loops or multiple edges is often distinguished from the graphs that satisfy these constraints by calling it a "multigraph" or "pseudograph".
In a graph with one vertex, all edges must be loops. Such a graph is called a bouquet.
Degree
For an undirected graph, the degree of a vertex is equal to the number of adjacent vertices.
A special case is a loop, which adds two to the degree. This can be understood by letting each connection of the loop edge count as its own adjacent vertex. In other words, a vertex with a loop "sees" itself as an adjacent vertex from both ends of the edge thus adding two, not one, to the degree.
For a directed graph, a loop adds one to the in degree and one to the out degree.
See also
Loops in Graph Theory
- Cycle (graph theory)
- Graph theory
- Glossary of graph theory
Loops in Topology
References
- Balakrishnan, V. K.; Graph Theory, McGraw-Hill; 1 edition (February 1, 1997). ISBN 0-07-005489-4.
- Bollobás, Béla; Modern Graph Theory, Springer; 1st edition (August 12, 2002). ISBN 0-387-98488-7.
- Diestel, Reinhard; Graph Theory, Springer; 2nd edition (February 18, 2000). ISBN 0-387-98976-5.
- Gross, Jonathon L, and Yellen, Jay; Graph Theory and Its Applications, CRC Press (December 30, 1998). ISBN 0-8493-3982-0.
- Gross, Jonathon L, and Yellen, Jay; (eds); Handbook of Graph Theory. CRC (December 29, 2003). ISBN 1-58488-090-2.
- Zwillinger, Daniel; CRC Standard Mathematical Tables and Formulae, Chapman & Hall/CRC; 31st edition (November 27, 2002). ISBN 1-58488-291-3.
External links
