CaRMetal

CaRMetal is an interactive geometry program which inherited the C.a.R. engine. The software has been created by Eric Hakenholz, in Java. CaRMetal is free, under GNU GPL license. It keeps an amount of functionality of C.a.R. but uses a different graphical interface which purportedly eliminates some intermediate dialogs and provides direct access to numerous effects. Constructions are done using a main palette, which contains some useful construction shortcuts in addition to the standard compass and ruler tools. These include perpendicular bisector, circle through three points, circumcircular arc through three points, and conic section through five points. Also interesting are the loci, functions, parametric curves, and implicit plots. Element thickness, color, label, and other attributes (including the so-called magnetic property) can be set using a separate panel.

CaRMetal
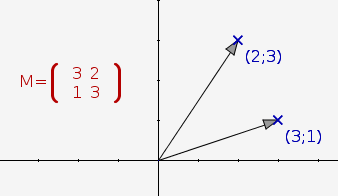
Two conic sections using CaRMetal
Original author(s)Eric Hakenholz
Developer(s)Eric Hakenholz, Patrice Debrabant, Pierre-Marc Mazat, Alain Busser
Initial releaseOctober 28, 2006 (2006-10-28)
Stable release
4.3.0 / January 5, 2019 (2019-01-05)
Repositorynone
Written inJava
PlatformJava
TypeInteractive geometry software
LicenseGNU General Public License
Websitecarmetal.org

CaRMetal also supports a configurable restricted construction palette and has assignment capabilities, which use an apparently unique feature called Monkey. CaRMetal has a scripting language (JavaScript) which allows the user to build rather complex figures like fractals. CaRMetal has several locales including French, English, Spanish, German, Italian, Dutch, Portuguese and Arabic.

Didactic interest

Anticipation
When one is constructing a parallel line, it follows the mouse, which makes it easy to emit conjectures even while the figure is still under construction.

When one chooses a tool like the parallel to a line through a point, or a circle, the intended object appears in yellow color and follows the mouse movements. This allows the user to make conjectures even before the construction is finished. This constant interaction between the pupil and the object of experimentation is in phase with modern theories about didactics and, in this view, CaRMetal is intended to be used by students.

Amodality

The windows which show the history, the tools palette, the properties of the selected object are around the figure and never above it. These windows are not modal windows in the sense that they never hide the construction. For example, whenever the user wants to change the color of a polygon, he sees the new color immediately.

Transformations

When a transformation (for example a macro) has been defined, such that it transforms points into points, this transformation can also be applied to curves. Once again, this allows the learning subject to see the properties of the transformation at a glance, even before the transformation has actually been applied.

Assignments
the Monkey button

The workbooks (see below) can be exported as html files, with a restricted tools palette (for example, leaving only the intersection and circle tools lets the pupil make compass-only construction). To create an assignment, the teacher chooses the initial objects, the objects to be created by the pupil, and writes a text explaining what is to be done. Since 2010, when the pupil has finished the construction and wants to test it, random variations are tested (with a tool called Monkey) and a quality note is attributed to the pupil (actually, a percentage of the good constructions amongst the variations).

Macros

The macros can be organized in a hierarchy of folders, which make it easy to transform CaRMetal into a tool allowing to explore non-euclidean geometries.

Special features

Workbooks

Since 2010, CaRMetal uses a folder system allowing one to put several figures in one folder, called "workbook". It is easy to navigate between the sheets of a workbook, to duplicate a sheet (or figure), to merge several workbooks into one. CaRMetal allows one to include picture files and JavaScript files into a figure. The file extension of a figure is zir like in C.a.R. (by the way, there is much compatibility between both software) and the file structure is a meta-description of the figure in the XML language. But a workbook is saved as a zipped folder containing all the zir figures, plus the included pictures (GIF, JPEG or PNG) and a preferences file.

Numeric display
An example of a matrix which can be changed in real time with the extremities of the vectors, and displayed with LaTeX.

It is possible to convert any numerical measure of the figure into text, for display purposes. For example, if a segment called 's1' is 4.5 unit long, writing

"The length of the segment is %s1%"

creates a character string which displays as The length of the segment is 4.5. This character string can be included into the figure but also set as the alias of an object (for example s1) or the name of an expression. Of course when one of the extremities of the segment is moved with the mouse, the text is edited in real time. This is called a dynamic text.

CaRMetal uses HotEqn and JLatexMath which are LaTeX parsers, and it is possible to write LaTeX formulae inside text objects. For example, if poly1 is a square, and one wishes to find a circle which area is the same as the square's one, one can build a text expression like this:

"The radius of the circle would be $\sqrt{\frac{%poly1%}{\pi}}\simeq %sqrt(poly1/pi)%$"

This can give a text such as this:

The strength of this feature comes from the fact that it is possible to mix up dynamic texts with LaTeX formulae, getting dynamic LaTeX(when the size of the square changes, the display changes too)!

3D
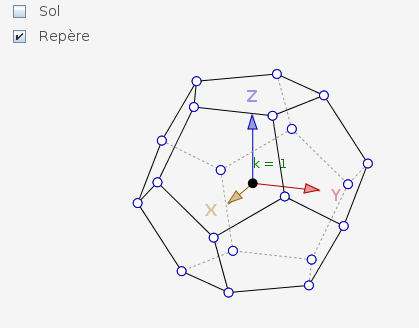
a dodecahedron can be turned with the mouse

CaRMetal allows the user to set some properties of the objects, like their color or the fact that they are visible or not, as conditional. Also each object can have a layer number. An important application of these features was the 2.5D mode of CaRMetal, emulating 3D geometry. Since the version 4.0 CaRMetal has a real 3D mode which comes up with a regular tetrahedron, a cube, a diamond and a regular dodecahedron. It is also possible to bind a point to the inside of a (3D) circle or polygon. This feature, inherited from C.a.R., is based on barycentric coordinates. Since the 4.1 version CaRMetal permits some turtle graphics (programmed in JavaScript) either in 2D or in 3D.

Magnetism

A point can be made magnetic with a distance and a list of objects it is attracted to whenever the point is sufficiently near one or several of these objects (sufficiently near means that the distance between them is less than the minimal distance which is a property of the point, and is measured in pixel units). For example, when a point is attracted to a finite set of points, which themselves are fixed, it can explore a finite geometry.

Network

Since 2013 there is the possibility to run one CaRMetal figure as server (typically, the teacher's one) and several as clients. Therefore, it is possible

  • to send one's figure to the server
  • for the server, to send a correct figure to a student who lost his, or cannot create it in the requested times
  • to collect data, geometrical or not, within one single figure (the server's one)
  • to manipulate the same figure at the same time, for several people who share their work
  • to send and receive JavaScript programs (see below)
  • to chat within a shared figure...

JavaScript inside CaRMetal

The script tool mixes up algorithmics and geometry. Such scripting tools exist also in DrGeo, Kig and Cinderella (software). To run a script, one clicks over the icon representing a traffic light. A script can be attached to one or several points, so that any movement of one of these points runs the script. This allows some kind of inverse kinematics much like with GeoLicia.

Variables

To create a geometric object in JavaScript it suffices to click on an icon representing the object. The JavaScript instruction appears in the editor, with predefined parameters. The user has then only to edit these, and does not have to use mnemotechnics. But when a geometric object is created, the variable which called the routine is really a character string, containing the name of the object.

For example,

a=Point(2,3);

creates a point, usually called P1 and the variable a contains the string "P1". This allows to refer to the point by its name. The coordinates of the point are initialized but the point can still move with the use of the mouse. It is also possible to create a point in procedural programming with

Point("A",2,3);

In this case, the name of the point is "A" (unless there be already an object called "A"), and no variable is set to the name "A".

Input-Output

To output a variable, there are four ways:

  1. Create an expression inside the figure (or display with a graphic mean such as an histogram);
  2. Print which opens a new window and prints the content of the variable in it;
  3. Println which also goes to the line;
  4. Alert which opens an alert window, which closes as soon as the user clicked on OK.

To input a variable, there is

  1. Input (you bet!) which opens an input window (with a text) and waits for the click on OK
  2. InteractiveInput which lets the user choose an object in the figure

This paradigm considers the variables of the program not necessarily as numeric or string variables but can act on graphic objects too. This is a common feature with Kig (but in this case, the language is Python (language)) and DrGeo (in this case, with Scheme (language)).

Strings

It is also possible to set the coordinates of a point as character strings written in the language of CaRMetal. For example, to have a point B which follows A except that B's coordinates are integer (to model a gaussian integer) one can write

a=Point("2.72","3.14");
b=Point("round(x_a)","round(y_a)");

Loops

As an example, the Sierpinski triangle can be built up as an iterated function system with this recursive script, which is rather short because of the already available graphic instructions such as MidPoint:

a=Point(-4,-2);
b=Point(4,-2);
c=Point(0,4);
m=Point(Math.random(),Math.random());
SetHide(m,true);
for(n=0;n<2000;n++){
	dice=Math.ceil(Math.random()*3);          //A 3-faces dice!
	switch(dice){
		case 1: {p=MidPoint(a,m); break;
		}
		case 2: {p=MidPoint(b,m); break;
		}
		case 3: {p=MidPoint(c,m); break;
		}
	}
	SetPointType(p,"point");
	m=p;
}

After the cloud of points has been built up (and even while the script is still running!) one can make A, B and C move with the mouse (or automatically with the Monkey): The triangle is dynamic!

JavaScript objects

CaRMetal can also use the JavaScript objects like

  1. arrays, useful to make statistics on geometric figures;
  2. date object, useful to measure time;
  3. String and RegExp objects, which make it easy to implement L-systems;
  4. General JavaScript objects can be used to create new geometric objects like complex numbers, matrices etc. This object-oriented programming works much like Kig's Python scripts, but as of today no one seems to have publish anything using that.
gollark: You'll need to ask birdzgoboom about offsite use of that...
gollark: I'll just upload all those, then.
gollark: Tatter?
gollark: ... hmm, in that case, maybe something *contrasting* with the teal (and with a different offfsite use policy) would be better.
gollark: Also, I'd prefer if the *background* were teal and the text white or something - see the actual site.

See also
  • C.a.R.
  • Compass-and-straightedge construction
  • Interactive geometry software

References
    • Vers des spécifications formelles : Fondements Mathématiques et Informatiques pour la Géométrie Dynamique, Bernard Genevès (PhD) PDF
    • Busser Alain. TP sous JavaScript avec CaRMetal. Bulletin de l’APMEP, 487 (2010), p. 191-199.
    • Busser Alain. Un an d’algorithmique avec CaRMetal en Seconde. MathémaTICE, 21 (2010) (online article: )
    • Martin Yves. Algorithmique et intégration des outils. Repères IREM, 79 (2010), p. 5-22.
    • Martin Yves. Géométrie repérée dynamique : une autre voie vers l’algébrisation ? MathémaTICE, 20 (2010) (available online: )
    • Martin Yves. Quand la géométrie dynamique rencontre la programmation. In Actes du colloque « Les mathématiciens et l’enseignement de leur discipline en France » (CIRM, Marseille/Luminy, 15-19 mars 2010) (video online: )
    • Martin Yves. CaRMetal, une géométrie dynamique enrichie. Expressions, 35 (2010), p. 165-272 PDF
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.