Brent–Kung adder
The Brent–Kung adder (BKA or BK), proposed in 1982,[1] is an advanced binary adder design, having a gate level depth of .
| Part of a series on | |||||||
| arithmetic logic circuits | |||||||
|---|---|---|---|---|---|---|---|
| Quick navigation | |||||||
|
Components
|
|||||||
|
Categories
|
|||||||
|
See also
|
|||||||
Introduction
The Brent–Kung adder is a parallel prefix adder (PPA) form of carry-lookahead adder (CLA). Proposed by Richard Peirce Brent and Hsiang Te Kung in 1982 it introduced higher regularity to the adder structure and has less wiring congestion leading to better performance and less necessary chip area to implement compared to the Kogge–Stone adder (KSA). It is also much quicker than ripple-carry adders (RCA).
Ripple-carry adders were the initial multi-bit adders which were developed in the early days and got their name from the ripple effect which the carry made while being propagated from right to left. The time taken for addition was directly proportional to the length of the bit being added. This is reverse in Brent–Kung adders where the carry is calculated in parallel thus reducing the addition time drastically. Further work has been done on Brent–Kung adders and other parallel adders to reduce the power consumption and chip area as well as to increase the speed thus making them suitable for low-power designs.
A Brent–Kung adder is a parallel adder made in a regular layout with an aim of minimizing the chip area and ease of manufacturing. The addition of n-bit number can be performed in time with a chip size of area thus making it a good-choice adder with constraints on area and maximizing the performance. Its symmetry and regular build structure reduces costs of production effectively and enable it to be used in pipeline architectures. In parallel adders the critical path is decided by computation of the carry from least significant bit (LSB) adder to the most significant bit (MSB) adder, therefore efforts are in reducing the critical path for the carry to reach the MSB.
Basic model outline
In general, most of the adders use carry-in and the corresponding bits of two numbers (A and B) to get the corresponding sum bit and carry-out - with ripple carry adders taking time for carry to reach MSB.
- Considering that A = an an-1 … a1 and B = bn bn-1 … b1 both be n-bit binary numbers.
- With sum being S = sn+1 sn … s1 and carry generated in each stage C = cn … c0 will be carry-in to next stages.
- For RCA, c0 = 0, and i the sum bit and carry bit generated are ci = gi ∨ (ai ∧ ci-1) ∨ (bi ∧ ci-1),
si = ai ⊕ bi ⊕ ci-1 for i = 1, 2, … n
sn+1 = cn respectively. - It is possible to transform the above ripple carry into carry-lookahead (CLA) by defining the carry bit i as c0 = 0,
ci = (ai ∧ bi) ∨ (pi ∧ ci-1) where
gi = ai ∧ bi and pi = ai ⊕ bi for i = 1, 2, … n. p and g are known as carry propagate and carry generate. This corresponds to the fact that the carry ci is either generated by ai and bi or propagated from the previous carry ci-1.
Brent and Kung further transformed the carry generation and propagation by defining an operator o as
(a1, b1) o (a2, b2) = (a1 ∨ (b1 ∧ a2), b1 ∧ b2).
- They also defined a function (Gi, Pi) = (g1, p1) for i = 1;
otherwise (gi, pi) o (Gi-1, Pi-1) for i = 2, 3, … n. It can be derived that Gi in the function is equivalent to ci. Also (Gn, Pn) can be non-recursively written as = (gn, pn) o (gn-1, pn-1) o … o (g1, p1).
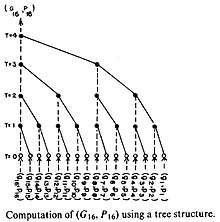
Taking advantage of the associativity of operator o (Gn, Pn) can be computed in a tree-like manner.
The design of the white nodes is obvious as they are just buffering the gi's and pi's, and the black nodes are performing operation defined by operator o, which is similar to a one bit adder.
- This tree-like propagation of carry reduces its critical path to that of tree height. As the carry tree height can be maximum of , the critical path of the Brent–Kung parallel adder is also , which is better than the normal adder performance of . The tree-based layout also reduces the chip area and redundant wiring required in general CLA-based adders.
Final processing stage
Using the carry propagation and generation transformation for working out addition and carry used by Brent and Kung, the performance of the adder increases considerably and also leads to an increase in regularity. The final sum can be calculated as follows: si = pi ⊕ ci-1
Low-power adder
The increase in performance in Brent–Kung adders is attributed to its tree structure of carry propagation which also leads to lower power consumption as the carry signal now has to travel through fewer stages, leading to less switching of transistors. Also, the decrease in amount of wiring and fan-out also contributes largely to its lower power consumption than CLA adders. A Brent–Kung adder can also be used in a pipeline manner which can further reduce the power consumption by reducing the depth of combinatorial logic and glitches stabilization.[1] The graph shows a low-power Brent–Kung adder.[2]
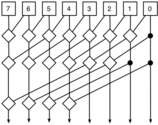
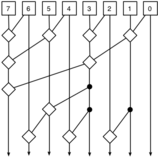
Comparison with Kogge–Stone adder
Advantages
Due to this type of adder requiring fewer modules to implement than the Kogge–Stone adder, the Brent–Kung adder is much simpler to build. It also contains far fewer connections to other modules, which also contributes to its simplicity.[3]
Disadvantages
One major disadvantage of this adder is fan-out. Fan-out may split and weaken the current propagating through the adder.[3]
References
- Brent, Richard Peirce; Kung, Hsiang Te (March 1982) [June 1979]. "A Regular Layout for Parallel Adders". IEEE Transactions on Computers. Department of Computer Sciences, Carnegie-Mellon University, USA. C-31 (3): 260–264. doi:10.1109/TC.1982.1675982. ISSN 0018-9340. CMS-CS-79-131.
- Alexander, Jonathan (2004). "VHDL Design Tips and Low Power Design Techniques". Retrieved 2018-04-21.
- Pointer, Robey (2012-11-14). "How to add numbers (part 2)". robey.lag.net. Archived from the original on 2018-04-21. Retrieved 2018-04-21.
Further reading
- Reynders, Nele; Dehaene, Wim (2015). Ultra-Low-Voltage Design of Energy-Efficient Digital Circuits. Analog Circuits And Signal Processing (ACSP) (1 ed.). Cham, Switzerland: Springer International Publishing AG Switzerland. doi:10.1007/978-3-319-16136-5. ISBN 978-3-319-16135-8. ISSN 1872-082X. LCCN 2015935431.