Boundary parallel

In mathematics, a closed n-manifold N embedded in an (n + 1)-manifold M is boundary parallel (or ∂-parallel, or peripheral) if there is an isotopy of N onto a boundary component of M.

An example

Consider the annulus ${\displaystyle I\times S^{1}}$. Let π denote the projection map

${\displaystyle \pi :I\times S^{1}\rightarrow S^{1},\qquad (x,z)\mapsto z.}$

If a circle S is embedded into the annulus so that π restricted to S is a bijection, then S is boundary parallel. (The converse is not true.)

If, on the other hand, a circle S is embedded into the annulus so that π restricted to S is not surjective, then S is not boundary parallel. (Again, the converse is not true.)

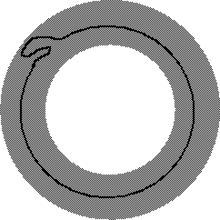
An example wherein π is not bijective on S, but S is ∂-parallel anyway.

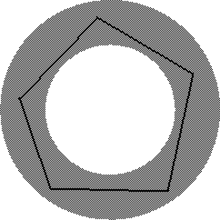
An example wherein π is bijective on S.

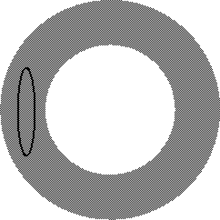
An example wherein π is not surjective on S.