Bingo card

Bingo cards are playing cards designed to facilitate the game of Bingo in its various forms around the world.

History

In the early 1500s the people of Italy began to play a game called "Lo Gioco del Lotto d'Italia," which literally means "The game of lotto of Italy." The game operated very much like a modern lottery as players placed bets on the chances of certain numbers being drawn. By the 1700s, a version of Lo Gioco del Lotto d'Italia was played in France, where paper cards were first used to keep track of numbers drawn by a caller.[1]

Before the advent of printing machines, numbers on bingo cards were either painted by hand or stamped using rubber stamps onto thick cardboard.[2] Cards were reusable, meaning players used tokens to mark called numbers. The number of unique cards was limited as randomization had to occur by hand. Before the advent of online Bingo, cards were printed on card stock and, increasingly, disposable paper.[3] While cardboard and paper cards are still in use, Bingo halls are turning more to "flimsies" (also called "throwaways") — a card inexpensively printed on very thin paper to overcome increasing cost — and electronic Bingo cards to overcome the difficulty with randomization.[4][5]

Types of Cards

There are two types of Bingo cards. One is a 5x5 grid meant for 75-ball Bingo, which is largely played in the U.S. The other uses a 9x3 grid for U.K. style "Housie" or 90-ball Bingo.[6]

75-ball Bingo Cards

Players use cards that feature five columns of five squares each, with every square containing a number (except the middle square, which is designated a "FREE" space). The columns are labeled "B" (numbers 1–15), "I" (numbers 16–30), "N" (numbers 31–45), "G" (numbers 46–60), and "O" (numbers 61–75).[7]

Randomization

A popular Bingo myth[8] claims that U.S. Bingo innovator Edwin S. Lowe contracted Columbia University professor Carl Leffler to create 6,000 random and unique Bingo cards. The effort is purported to have driven Leffler insane. Manual random permutation is an onerous and time-consuming task that limited the number of Bingo cards available for play for centuries.

The calculation of random permutations is a matter of statistics principally relying on the use of factorial calculations. In its simplest sense, the number of unique "B" columns assumes that all 15 numbers are available for the first row. That only 14 of the numbers are available for the second row (one having been consumed for the first row). And that only 13, 12, and 11 numbers are available for each of the third, fourth, and fifth rows. Thus, the number of unique "B" (and "I", "G", and "O", respectively) columns is (15*14*13*12*11) = 360,360. The combinations of the "N" column differ due to the use of the free space. Therefore, it has only (15*14*13*12) = 32,760 unique combinations. The product of the five rows (360,3604 * 32,760) describes the total number of unique playing cards. That number is 552,446,474,061,128,648,601,600,000 simplified as 5.52x1026 or 552 septillion.

Printing a complete set of Bingo cards is impossible for all practical purposes. If one trillion cards could be printed each second, a printer would require more than seventeen thousand years to print just one set. However, while the number combination of each card is unique, the number of winning cards is not. If a winning game using e.g. row #3 requires the number set B10, I16, G59, and O69, there are 333,105,095,983,435,776 (333 quadrillion) winning cards. Therefore, calculation of the number of Bingo cards is more practical from the point of view of calculating the number of unique winning cards.

For example, in a simple one-pattern game of Bingo a winning card may be the first person to complete row #3. Because the "N" column contains a free space, the maximum number of cards that guarantee a unique winner is (15*15*15*15) = 50,625. Because the players need to only focus on row #3, the remaining numbers in rows #1, #2, #4, and #5 are statistically insignificant for purposes of game play and can be selected in any manner as long as no number is duplicated on any card.

Perhaps the most common pattern set, known as "Straight-line Bingo" is completing any of the five rows, columns, or either of the main diagonals.[5] In this case the possibility of multiple winning cards is unavoidable because any one of twelve patterns on every card can win the game. But not all 552 septillion cards need to be in play. Any given set of numbers in a column (e.g., 15, 3, 14, 5, 12 in the "B" column) can be represented in any of 5! (for the "B", "I", "G", and "O" columns. 4! for the "N" column) or 120 different ways. These combinations are all statistically redundant. Therefore, the total number of cards can be reduced by a factor of (5!4 * 4!) = 4,976,640,000 for a total unique winning card set of 111,007,923,832,370,565 or 111 quadrillion. (Still impossibly enormous, but our eager printer described above would only need 1.29 days to complete the task.)

The challenge of a multiple-pattern game is selecting a winner wherein a tie is possible. The solution is to name the player who shouts "Bingo!" first, is the winner. However, it is more practical and manageable to use card sets that avoid multiple-pattern games. The single-pattern #3 row has already been mentioned, but its limited card set causes problems for the emerging online Bingo culture. Larger patterns, e.g. a diamond pattern consisting of cell positions B3, I2 and I4, N1 and N5, G2 and G4, and O3, are often used by online Bingo games to permit large number of players while ensuring only one player can win. (A unique winner is further desirable for online play where network delays and other communication interference can unfairly affect multiple winning cards. The winner would be determined by the first person to click the "Bingo!" button (emulating the shout of "Bingo!" during a live game).) In this case the number of unique winning cards is calculated as (152*(15*14)3/23) = 260,465,625 (260 million). The division by two for each of the "I", "N", and "G" columns is necessary to once again remove redundant number combinations, such as [31,#,#,#,45] and [45,#,#,#,31] in the N column.

90-ball bingo cards
A typical housie/Bingo ticket

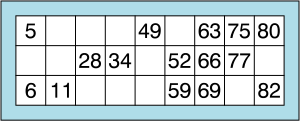
[9] In UK bingo, or Housie, cards are usually called "tickets." The cards contain three rows and nine columns. Each row contains five numbers and four blank spaces randomly distributed along the row. Numbers are apportioned by column (1–9, 10–19, 20–29, 30–39, 40–49, 50–59, 60–69, 70–79 and 80–90).

Other Types of Cards
  • Break Open
gollark: ```haskellinstance Semigroup a => Semigroup [a] where (<>) = zipWith (<>)```
gollark: Oh, right.
gollark: Er, `++`.
gollark: Surely the only valid list semigrouporwhatever is `<>`?
gollark: `(<>) (++)`

See also

References
  • Young, William H. and Nancy K. The Great Depression in America: A Cultural Encyclopedia, Volume 1. Greenwood Publishing Group, 2007. ISBN 978-0-313-33521-1.

Footnotes
  1. Crossland, Drake. "Bingo:A Game's Journey Through History". EZinearticles.com.
  2. "Bingo Card History". VirtualBingo. Retrieved 2012-12-08.
  3. "Bingo Cards". BettingExpert. Retrieved 2012-12-08.
  4. "Types of Bingo Cards". VirtualBingo. Retrieved 2012-12-08.
  5. Andrew Bowser. "Bingo Equipment". How Stuff Works. Retrieved 2012-12-08.
  6. Hoeft, Mike (2014). The bingo queens of Oneida : how two moms started tribal gaming in Wisconsin (First edition. ed.). ISBN 0870206524. Retrieved 20 January 2016.
  7. John, Player (1 January 2014). "Gala Bingo Mobile App: play wherever you are". Retrieved 20 January 2016.
  8. "Bingo Myths: Fact or Fiction?". My Casino Strategy. Retrieved 2012-12-08.
  9. "bingobonuspage:What are the different Bingo game types?". Retrieved 12 April 2016.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.