Binary GCD algorithm

The binary GCD algorithm, also known as Stein's algorithm, is an algorithm that computes the greatest common divisor of two nonnegative integers. Stein's algorithm uses simpler arithmetic operations than the conventional Euclidean algorithm; it replaces division with arithmetic shifts, comparisons, and subtraction. Although the algorithm was first published by the Israeli physicist and programmer Josef Stein in 1967,[1] it may have been known in 1st-century China.[2]

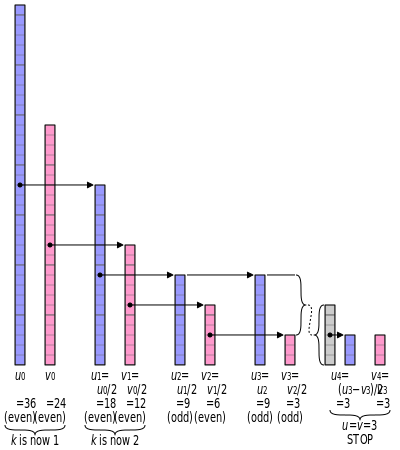
Visualisation of using the binary GCD algorithm to find the greatest common divisor (GCD) of 36 and 24. Thus, the GCD is 22 × 3 = 12.

Algorithm

The algorithm reduces the problem of finding the GCD of two nonnegative numbers v and u by repeatedly applying these identities:

  • gcd(0, v) = v, because everything divides zero, and v is the largest number that divides v. Similarly, gcd(u, 0) = u.
  • gcd(2u, 2v) = 2·gcd(u, v)
  • gcd(2u, v) = gcd(u, v), if v is odd (2 is not a common divisor). Similarly, gcd(u, 2v) = gcd(u, v) if u is odd.
  • gcd(u, v) = gcd(|u − v|, min(u, v)), if u and v are both odd.

For word-sized integers, the algorithm requires a number of machine operations on the order of log(max(u, v)).

Asymptotically, the algorithm requires O(n2)[3] worst-case time, where n is the number of bits in the larger of the two numbers: although each step reduces at least one of the operands by at least a factor of 2, the subtract and shift operations take linear time (one machine operation per word of the representation).

An extended binary GCD, analogous to the extended Euclidean algorithm, can provide the Bézout coefficents in addition to the GCD, i.e. integers a and b such that a·u + b·v = gcd(u, v).[4][5]

Implementation

Recursive version in C

Following is a recursive implementation of the algorithm in C. The implementation is similar to the description of the algorithm given above. It uses two arguments u and v. All but one of the recursive calls are tail recursive.

unsigned int gcd(unsigned int u, unsigned int v)
{
    // simple cases (termination)
    if (u == v)
        return u;

    if (u == 0)
        return v;

    if (v == 0)
        return u;

    // look for factors of 2
    if (~u & 1) // u is even
        if (v & 1) // v is odd
            return gcd(u >> 1, v);
        else // both u and v are even
            return gcd(u >> 1, v >> 1) << 1;

    if (~v & 1) // u is odd, v is even
        return gcd(u, v >> 1);

    // reduce larger argument
    if (u > v)
        return gcd((u - v) >> 1, v);

    return gcd((v - u) >> 1, u);
}

Iterative version in Rust

Following is an implementation of the algorithm in Rust, adapted from uutils. It removes all common factors of 2, using identity 2 and a fast bitwise primitive (u64::trailing_zeros), then computes the GCD of the remaining numbers using identities 3 and 4, combining these to form the final answer.

pub fn gcd(mut u: u64, mut v: u64) -> u64 {
    use std::cmp::min;
    use std::mem::swap;

    // Base cases: gcd(n, 0) = gcd(0, n) = n
    if u == 0 {
        return v;
    } else if v == 0 {
        return u;
    }

    // Using identities 2 and 3:
    // gcd(2ⁱ u, 2ʲ v) = 2ᵏ gcd(u, v) with u, v odd and k = min(i, j)
    // 2ᵏ is the greatest power of two that divides both u and v
    let i = u.trailing_zeros();  u >>= i;
    let j = v.trailing_zeros();  v >>= j;
    let k = min(i, j);

    loop {
        // u and v are odd at the start of the loop
        debug_assert!(u % 2 == 1, "u = {} is even", u);
        debug_assert!(v % 2 == 1, "v = {} is even", v);

        // Swap if necessary so u <= v
        if u > v {
            swap(&mut u, &mut v);
        }

        // Using identity 4 (gcd(u, v) = gcd(|v-u|, min(u, v))
        v -= u;

        if v == 0 {
            return u << k;
        }

        // Identity 3: gcd(u, 2ʲ v) = gcd(u, v) (u is known to be odd)
        v >>= v.trailing_zeros();
    }
}

Efficiency

Akhavi and Vallée proved that binary GCD is about 60% more efficient on average, in terms of the number of bit operations, than the Euclidean algorithm.[6]

This algorithm achieves the same asymptotic complexity as the Euclidean algorithm, though neither is the fastest for arbitrary-precision arithmetic, as they both take quadratic time (with regards to the input's size, i.e. the number of digits). Instead, recursive methods that combine ideas from the binary GCD algorithm with the Schönhage–Strassen algorithm for fast integer multiplication can find GCDs in near-linear time.[7]

Historical description

An algorithm for computing the GCD of two numbers was described in the ancient Chinese mathematics book The Nine Chapters on the Mathematical Art. The original algorithm was used to reduce a fraction. The description reads:

"If possible halve it; otherwise, take the denominator and the numerator, subtract the lesser from the greater, and do that alternately to make them the same. Reduce by the same number."

This description looks like a normal Euclidean algorithm, but there is ambiguity in the phrase "if possible halve it". The traditional interpretation is that this only applies when 'both' numbers are even, implying the algorithm is just slightly inferior to the Euclidean algorithm (for using subtraction instead of division). But the phrase may mean dividing by 2 should 'either' of the numbers become even, in which case it is the binary GCD algorithm.

See also

References
  1. Stein, J. (1967), "Computational problems associated with Racah algebra", Journal of Computational Physics, 1 (3): 397–405, doi:10.1016/0021-9991(67)90047-2, ISSN 0021-9991
  2. Knuth, Donald (1998), Seminumerical Algorithms, The Art of Computer Programming, 2 (3rd ed.), Addison-Wesley, ISBN 978-0-201-89684-8
  3. "GNU MP 6.1.2: Binary GCD".
  4. Knuth 1998, p. 646, answer to exercise 39 of section 4.5.2
  5. "Handbook of Applied Cryptography" (PDF). Retrieved 2017-09-09.
  6. Akhavi, Ali; Vallée, Brigitte (2000), "Average Bit-Complexity of Euclidean Algorithms", Proceedings ICALP'00, Lecture Notes Computer Science 1853: 373–387, CiteSeerX: 10.1.1.42.7616, archived from the original on 2006-10-02
  7. Stehlé, Damien; Zimmermann, Paul (2004), "A binary recursive gcd algorithm", Algorithmic number theory (PDF), Lecture Notes in Comput. Sci., 3076, Springer, Berlin, pp. 411–425, CiteSeerX 10.1.1.107.8612, doi:10.1007/978-3-540-24847-7_31, ISBN 978-3-540-22156-2, MR 2138011.

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.