Binary data
Binary data is data whose unit can take on only two possible states, traditionally labeled as 0 and 1 in accordance with the binary numeral system and Boolean algebra.
Binary data occurs in many different technical and scientific fields, where it can be called by different names:
- "bit" (binary digit) in computer science,
- "truth value" in mathematical logic and related domains,
- "binary variable" in statistics.
Mathematical and combinatoric foundations
A discrete variable that can take only one state contains zero information, and 2 is the next natural number after 1. That is why the bit, a variable with only two possible values, is a standard primary unit of information.
A collection of n bits may have 2n states: see binary number for details. Number of states of a collection of discrete variables depends exponentially on the number of variables, and only as a power law on number of states of each variable. Ten bits have more (1024) states than three decimal digits (1000). 10k bits are more than sufficient to represent an information (a number or anything else) that requires 3k decimal digits, so information contained in discrete variables with 3, 4, 5, 6, 7, 8, 9, 10… states can be ever superseded by allocating two, three, or four times more bits. So, the use of any other small number than 2 does not provide an advantage.
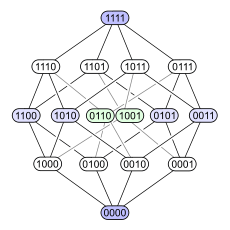
Moreover, Boolean algebra provides a convenient mathematical structure for collection of bits, with a semantic of a collection of propositional variables. Boolean algebra operations are known as "bitwise operations" in computer science. Boolean functions are also well-studied theoretically and easily implementable, either with computer programs or by so-named logic gates in digital electronics. This contributes to the use of bits to represent different data, even those originally not binary.
In statistics
In statistics, binary data is a statistical data type consisting of categorical data that can take exactly two possible values, such as "A" and "B", or "heads" and "tails". As a form of categorical data, binary data is nominal data, meaning they represent qualitatively different values that cannot be compared numerically. However, binary data is frequently converted to count data by considering one of the two values as "success" and representing the outcomes as 1 or 0, which corresponds to counting the number of successes in a single trial: 1 (success) or 0 (failure); see § Counting.
Often, binary data is used to represent one of two conceptually opposed values, e.g:
- the outcome of an experiment ("success" or "failure")
- the response to a yes-no question ("yes" or "no")
- presence or absence of some feature ("is present" or "is not present")
- the truth or falsehood of a proposition ("true" or "false", "correct" or "incorrect")
However, it can also be used for data that is assumed to have only two possible values, even if they are not conceptually opposed or conceptually represent all possible values in the space. For example, binary data is often used to represent the party choices of voters in elections in the United States, i.e. Republican or Democratic. In this case, there is no inherent reason why only two political parties should exist, and indeed, other parties do exist in the U.S., but they are so minor that they are generally simply ignored. Modeling continuous data (or categorical data of more than 2 categories) as a binary variable for analysis purposes is called dichotomization (creating a dichotomy). Like all discretization, it involves discretization error, but the goal is to learn something valuable despite the error: treating it as negligible for the purpose at hand, but remembering that it cannot be assumed to be negligible in general.
Binary variables
A binary variable is a random variable of binary type, meaning with two possible values. Independent and identically distributed (i.i.d.) binary variables follow a Bernoulli distribution, but in general binary data need not come from i.i.d. variables. Total counts of i.i.d. binary variables (equivalently, sums of i.i.d. binary variables coded as 1 or 0) follow a binomial distribution, but when binary variables are not i.i.d., the distribution need not be binomial.
Counting
Like categorical data, binary data can be converted to a vector of count data by writing one coordinate for each possible value, and counting 1 for the value that occurs, and 0 for the value that does not occur.[1] For example, if the values are A and B, then the data set A, A, B can be represented in counts as (1, 0), (1, 0), (0, 1). Once converted to counts, binary data can be grouped and the counts added. For instance, if the set A, A, B is grouped, the total counts are (2, 1): 2 A's and 1 B (out of 3 trials).
Since there are only two possible values, this can be simplified to a single count (a scalar value) by considering one value as "success" and the other as "failure", coding a value of the success as 1 and of the failure as 0. For example, if the value A is considered "success" (and thus B is considered "failure"), the data set A, A, B would be represented as 1, 1, 0. When this is grouped, the values are added, while the number of trial is generally tracked implicitly. For example, A, A, B would be grouped as 1 + 1 + 0 = 2 successes (out of }} trials). Going the other way, count data with is binary data, with the two classes being 0 (failure) or 1 (success).
Counts of i.i.d. binary variables follow a binomial distribution, with the total number of trials (points in the grouped data).
Regression
Regression analysis on predicted outcomes that are binary variables is known as binary regression; when binary data is converted to count data and modeled as i.i.d. variables (so they have a binomial distribution), binomial regression can be used. The most common regression methods for binary data are logistic regression, probit regression, or related types of binary choice models.
Similarly, counts of i.i.d. categorical variables with more than two categories can be modeled with a multinomial regression. Counts of non-i.i.d. binary data can be modeled by more complicated distributions, such as the beta-binomial distribution (a compound distribution). Alternatively, the relationship can be modeled without needing to explicitly model the distribution of the output variable using techniques from generalized linear models (GLM), such as quasi-likelihood and a quasibinomial model; see Overdispersion § Binomial.
In computer science

In modern computers, binary data refers to any data represented in binary form rather than interpreted on a higher level or converted into some other form. At the lowest level, bits are stored in a bistable device such as a flip-flop. While most binary data has symbolic meaning (except for don't cares) not all binary data is numeric. Some binary data corresponds to computer instructions, such as the data within processor registers decoded by the control unit along the fetch-decode-execute cycle. Computers rarely modify individual bits for performance reasons. Instead, data is aligned in groups of a fixed number of bits, usually 1 byte (8 bits). Hence, "binary data" in computers are actually sequences of bytes. On a higher level, data is accessed in groups of 1 word (4 bytes) for 32-bit systems and 2 words for 64-bit systems.
In applied computer science and in the information technology field, the term binary data is often specifically opposed to text-based data, referring to any sort of data that cannot be interpreted as text. The "text" vs. "binary" distinction can sometimes refer to the semantic content of a file (e.g. a written document vs. a digital image). However, it often refers specifically to whether the individual bytes of a file are interpretable as text (see character encoding) or cannot so be interpreted. When this last meaning is intended, the more specific terms binary format and text(ual) format are sometimes used. Semantically textual data can be represented in binary format (e.g. when compressed or in certain formats that intermix various sorts of formatting codes, as in the DOC format used by Microsoft Word); contrarily, image data is sometimes represented in textual format (e.g. the X PixMap image format used in the X Window System).
See also
- Bit array
- Bernoulli distribution
- Boolean data type
- Computer memory
- Categorical data
- Qualitative data
References
- Agresti, Alan (2012). "1.2.2 Multinomial Distribution". Categorical Data Analysis (3rd ed.). Wiley. p. 6. ISBN 978-0470463635.CS1 maint: ref=harv (link)