Bernstein–Vazirani algorithm

The Bernstein–Vazirani algorithm, which solves the Bernstein–Vazirani problem is a quantum algorithm invented by Ethan Bernstein and Umesh Vazirani in 1992.[1] It's a restricted version of the Deutsch–Jozsa algorithm where instead of distinguishing between two different classes of functions, it tries to learn a string encoded in a function.[2] The Bernstein–Vazirani algorithm was designed to prove an oracle separation between complexity classes BQP and BPP.[1]

Problem statement

Given an oracle that implements some function ${\displaystyle f\colon \{0,1\}^{n}\rightarrow \{0,1\}}$, It is promised that the function ${\displaystyle f(x)}$ is a dot product between ${\displaystyle x}$ and a secret string ${\displaystyle s\in \{0,1\}^{n}}$ modulo 2. ${\displaystyle f(x)=x\cdot s=x_{1}s_{1}+x_{2}s_{2}+\cdots +x_{n}s_{n}}$, find ${\displaystyle s}$.

Algorithm

Classically, the most efficient method to find the secret string is by evaluating the function ${\displaystyle n}$ times where ${\displaystyle x=2^{i}}$, ${\displaystyle i\in \{0,1,...,n-1\}}$[2]

${\displaystyle {\begin{aligned}f(1000\cdots 0_{n})&=s_{1}\\f(0100\cdots 0_{n})&=s_{2}\\f(0010\cdots 0_{n})&=s_{3}\\&\,\,\,\vdots \\f(0000\cdots 1_{n})&=s_{n}\\\end{aligned}}}$

In contrast to the classical solution which needs at least ${\displaystyle n}$ queries of the function to find ${\displaystyle s}$, only one query is needed using quantum computing. The quantum algorithm is as follows: [2]

Apply a Hadamard transform to the ${\displaystyle n}$ qubit state ${\displaystyle |0\rangle ^{\otimes n}}$ to get

${\displaystyle {\frac {1}{\sqrt {2^{n}}}}\sum _{x=0}^{2^{n}-1}|x\rangle .}$

Perform a controlled negation of every state in the superposition generated by the previous Hadamard transformation for which the oracle when applied to this state returns 1. This transforms the superposition into

${\displaystyle {\frac {1}{\sqrt {2^{n}}}}\sum _{x=0}^{2^{n}-1}(-1)^{f(x)}|x\rangle .}$

Another Hadamard transform is applied to each qubit which makes it so that for qubits where ${\displaystyle s_{i}=1}$, its state is converted from ${\displaystyle |-\rangle }$ to ${\displaystyle |1\rangle }$ and for qubits where ${\displaystyle s_{i}=0}$, its state is converted from ${\displaystyle |+\rangle }$ to ${\displaystyle |0\rangle }$.

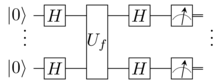
To obtain ${\displaystyle s}$, a measurement on the Standard basis (${\displaystyle \{|0\rangle ,|1\rangle \}}$) is performed on the qubits. Graphically algorithm may be represented by the following diagram:

Scheme of the algorithm

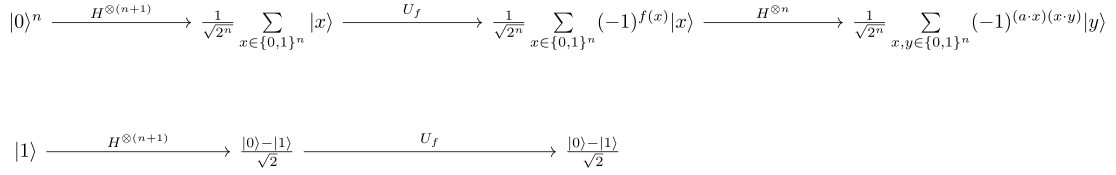
Where ${\displaystyle H^{\otimes n}}$ is the Hadamard transform.

See also

• Hidden Linear Function problem

References

1. Ethan Bernstein and Umesh Vazirani (1997). "Quantum Complexity Theory". SIAM Journal on Computing. 26 (5): 1411–1473. doi:10.1137/S0097539796300921.
2. S D Fallek, C D Herold, B J McMahon, K M Maller, K R Brown, and J M Amini (2016). "Transport implementation of the Bernstein–Vazirani algorithm with ion qubits". New Journal of Physics. 18. doi:10.1088/1367-2630/aab341.CS1 maint: multiple names: authors list (link)