6-8 duoprism
In geometry of 4 dimensions, a 6-8 duoprism, a duoprism and 4-polytope resulting from the Cartesian product of a hexagon and an octagon.
| 6-8 duoprism | |
|---|---|
| Type | Prismatic uniform polychoron |
| Schläfli symbol | {6}×{8} {6}×t{4} t{3}×{8} t{3}×t{4} |
| Coxeter diagram | |
| Cells | 6 octagonal prisms, 8 hexagonal prisms |
| Faces | 48 squares 6 octagons 8 hexagons |
| Edges | 96 |
| Vertices | 48 |
| Vertex figure | Digonal disphenoid |
| Symmetry | [6,2,8], order 192 |
| Dual | 6-8 duopyramid |
| Properties | convex, vertex-uniform |
Images
| Image |  |
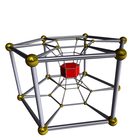 |
|---|---|---|
| Center | Octagonal prism | Hexagonal prism |
6-8 duopyramid
| 6-8 duopyramid | |
|---|---|
| Type | duopyramid |
| Schläfli symbol | {6}+{8} {6}+t{4} t{3}+{8} t{3}+t{4} |
| Coxeter-Dynkin diagram | |
| Cells | 48 digonal disphenoids |
| Faces | 96 isosceles triangles |
| Edges | 62 (48+6+8) |
| Vertices | 14 (6+8) |
| Symmetry | [6,2,8], order 192 |
| Dual | 6-8 duoprism |
| Properties | convex, facet-transitive |
The dual of a 6-8 duoprism is called a 6-8 duopyramid. It has 48 digonal disphenoid cells, 96 isosceles triangular faces, 62 edges, and 14 vertices.
Related polytopes
The 3-4 duoantiprism is an alternation of the 6-8 duoprism, but is not uniform. It has a highest symmetry construction of order 96, with 40 cells composed of 6 square antiprisms, 8 octahedra (as triangular antiprisms), and 24 tetrahedra (as digonal disphenoids). There exists a construction with uniform square antiprisms with an edge length ratio of 1 : 1.456, and also with regular octahedra with an edge length ratio of 0.663 : 1.

Vertex figure for the 3-4 duoantiprism
Also related is the bialternatosnub 3-4 duoprism, constructed by removing alternating long rectangles from the octagons, but is also not uniform. It has a highest symmetry construction of order 48, with 6 rectangular trapezoprisms (topologically equivalent to a cube but with D2d symmetry), 4 octahedra (as triangular antiprisms), 4 triangular prisms (both from the hexagonal prisms), with 24 triangular prisms (as C2v-symmetry wedges) filling the gaps. Its vertex figure is a Cs-symmetric polyhedron formed by augmenting a tetrahedron on one of the square pyramid's triangular faces.
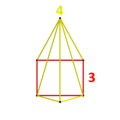
Vertex figure for the bialternatosnub 3-4 duoprism
See also
- Polytope and 4-polytope
- Convex regular 4-polytope
- Duocylinder
- Tesseract
Notes
References
- Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N. W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Catalogue of Convex Polychora, section 6, George Olshevsky.
External links
- The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
- Polygloss – glossary of higher-dimensional terms
- Exploring Hyperspace with the Geometric Product