Right angle

In geometry and trigonometry, a right angle is an angle of exactly 90° (degrees),[1] corresponding to a quarter turn.[2] If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles.[3] The term is a calque of Latin angulus rectus; here rectus means "upright", referring to the vertical perpendicular to a horizontal base line.

For other uses, see Right angle (disambiguation).
A right angle is equal to 90 degrees.
A line segment (AB) drawn so that it forms right angles with a line (CD).

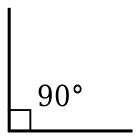
Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to vectors. The presence of a right angle in a triangle is the defining factor for right triangles,[4] making the right angle basic to trigonometry.

Etymology

The meaning of "right" in "right angle" possibly refers to the latin adjective rectus, which can be translated into erect, straight, upright or perpendicular. A Greek equvalent is orthos, which means straight or perpendicular (see orthogonality).

The term right angle therefore does not refer to right and left handedness, and thus there is no corresponding mathematical concept called a left angle. For reference, the corresponding Greek and Latin words for parts on the right handed side of the body are dexios and dexter, respectively.

In elementary geometry

A rectangle is a quadrilateral with four right angles. A square has four right angles, in addition to equal-length sides.

The Pythagorean theorem states how to determine when a triangle is a right triangle.

Symbols
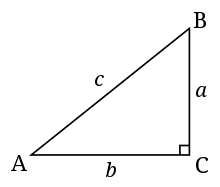
Right triangle, with the right angle shown via a small square.
Another option of diagrammatically indicating a right angle, using an angle curve and a small dot.

In Unicode, the symbol for a right angle is U+221F ∟ RIGHT ANGLE (HTML ∟ · ∟). It should not be confused with the similarly shaped symbol U+231E ⌞ BOTTOM LEFT CORNER (HTML ⌞ · ⌞, ⌞). Related symbols are U+22BE ⊾ RIGHT ANGLE WITH ARC (HTML ⊾ · ⊾), U+299C ⦜ RIGHT ANGLE VARIANT WITH SQUARE (HTML ⦜ · ⦜), and U+299D ⦝ MEASURED RIGHT ANGLE WITH DOT (HTML ⦝ · ⦝).[5]

In diagrams, the fact that an angle is a right angle is usually expressed by adding a small right angle that forms a square with the angle in the diagram, as seen in the diagram of a right triangle (in British English, a right-angled triangle) to the right. The symbol for a measured angle, an arc, with a dot, is used in some European countries, including German-speaking countries and Poland, as an alternative symbol for a right angle.[6]

Euclid

Right angles are fundamental in Euclid's Elements. They are defined in Book 1, definition 10, which also defines perpendicular lines. Definition 10 does not use numerical degree measurements but rather touches at the very heart of what a right angle is, namely two straight lines intersecting to form two equal and adjacent angles.[7] The straight lines which form right angles are called perpendicular.[8] Euclid uses right angles in definitions 11 and 12 to define acute angles (those smaller than a right angle) and obtuse angles (those greater than a right angle).[9] Two angles are called complementary if their sum is a right angle.[10]

Book 1 Postulate 4 states that all right angles are equal, which allows Euclid to use a right angle as a unit to measure other angles with. Euclid's commentator Proclus gave a proof of this postulate using the previous postulates, but it may be argued that this proof makes use of some hidden assumptions. Saccheri gave a proof as well but using a more explicit assumption. In Hilbert's axiomatization of geometry this statement is given as a theorem, but only after much groundwork. One may argue that, even if postulate 4 can be proven from the preceding ones, in the order that Euclid presents his material it is necessary to include it since without it postulate 5, which uses the right angle as a unit of measure, makes no sense.[11]

Conversion to other units

A right angle may be expressed in different units:

Rule of 3-4-5

Throughout history, carpenters and masons have known a quick way to confirm if an angle is a true "right angle". It is based on the most widely known Pythagorean triple (3, 4, 5) and so called the "rule of 3-4-5". From the angle in question, running a straight line along one side exactly 3 units in length, and along the second side exactly 4 units in length, will create a hypotenuse (the longer line opposite the right angle that connects the two measured endpoints) of exactly 5 units in length. This measurement can be made quickly and without technical instruments. The geometric law behind the measurement is the Pythagorean theorem ("The square of the hypotenuse of a right triangle is equal to the sum of the squares of the two adjacent sides").

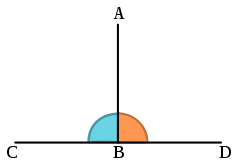
Thales' theorem
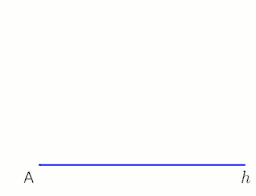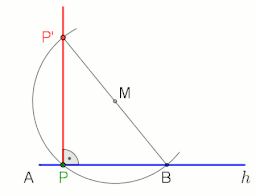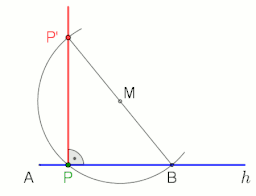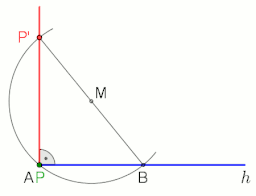
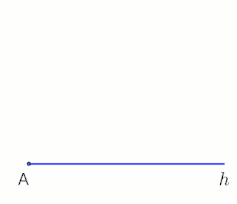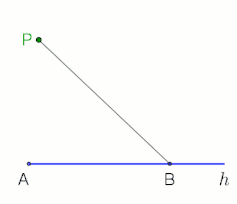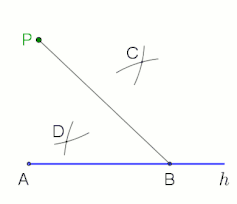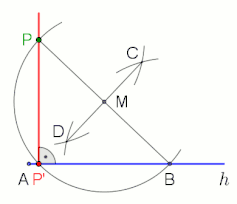
Construction of the perpendicular to the half-line h from the point P (applicable not only at the end point A, M is freely selectable), animation at the end with pause 10 s
Alternative construction if P outside of the half-line h and the distance A to P' is small (B is freely selectable),
animation at the end with pause 10 s

Thales' theorem states that an angle inscribed in a semicircle (with a vertex on the semicircle and its defining rays going through the endpoints of the semicircle) is a right angle.

Two application examples in which the right angle and the Thales' theorem are included (see animations).

gollark: There are tens of thousands (order of magnitude) of pages of laws I'm bound to follow and *I don't know what they are* and **cannot** know what they are.
gollark: Mostly sane? MOSTLY SANE?
gollark: It does have the constant acid-storms, but what can you do.
gollark: GTech™ isolated space-time environment 186 doesn't have winter!
gollark: These are empty of all other human life.

See also

References
  1. "Right Angle". Math Open Reference. Retrieved 26 April 2017.
  2. Wentworth p. 11
  3. Wentworth p. 8
  4. Wentworth p. 40
  5. Unicode 5.2 Character Code Charts Mathematical Operators, Miscellaneous Mathematical Symbols-B
  6. Müller-Philipp, Susanne; Gorski, Hans-Joachim (2011). Leitfaden Geometrie [Handbook Geometry] (in German). Springer. ISBN 9783834886163.
  7. Heath p. 181
  8. Heath p. 181
  9. Heath p. 181
  10. Wentworth p. 9
  11. Heath pp. 200-201 for the paragraph
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.