Shortest SHA-3 output

Question

I noticed in the new SHA-3 standard that it has a variable output size. Knowing that longer output is obviously better (higher entropy), what is theoretical the lower limit of the output size? Can my hashed output, e.g. be 8 bits long? I know for most scenarios this would not be secure.

Answer 1

You have a misconception:
With SHA3/Keccak, being a bit strange compared to previous hash functions, output size is not comparable to security. A certain security level requires a minimum output size, but the output can be made longer without increasing the security as hash.

The minimum hash size (of Keccak in general, not of the standardized subset called SHA3) is 1 bit:

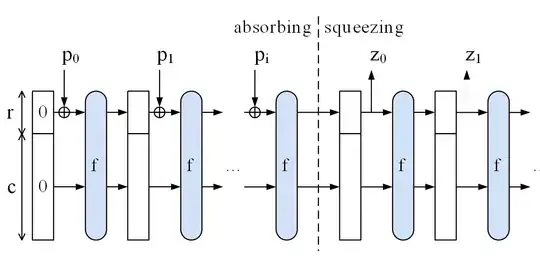
In the sponge construction the value of the sum c+r is restricted, but how much of it is c and how much r is freely choosable. Make r=1 and do only one iteration in the squeezing part (after the vertical line), then the hash output z0 has exactly 1 bit.

Answer 2

The SHA-3 standard is both old and new.

It's "old" because the competition for selecting the SHA-3 hash function began back in 2009 and we know since 2012 that Keccak won.

On the other hand, the standardization of SHA-3 is fairly new, considering FIPS-202 was standardized in August 2015.

If you want to use SHA-3, the shortest output length is 224 bits (SHA3-224), the longest output lenght for SHA-3 is 512-bit (SHA3-512).

However FIPS-202: SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions also defines two exentdible output functions (XOFs): SHAKE128 and SHAKE256 which have both a variable output length. Note that SHAKE128-256 isn't the same as SHA3-256 due to different padding.

The SHAKE functions allow arbitrary output lengths, as long as Keccak supports it. As Keccak is based on the sponge construction abitrary long outputs are no problem, however arbitrary short outputs can be obtained by simple truncation. The SHAKE functions accept the digest length in bits and don't perform any lower-bound checking, meaning that 1 bit is the shortest possible output of these functions.

Answer 3

If you look at FIPS 202 (the SHA-3 standard document), the SHAKE extendable output functions (XOFs) are defined like this (pp. 20-21):

SHAKE128(M, d) = KECCAK[256](M || 1111, d),
SHAKE256(M, d) = KECCAK[512](M || 1111, d).

...where M is the message to be hashed and d is the desired output length. The KECCAK function is defined in page 20:

KECCAK[c](N, d) = SPONGE[KECCAK-p[1600, 24], pad10*1, 1600–c](N, d).

The SPONGE algorithm is defined in p. 18, and they specify that the value of d can be any non-negative integer.

It follows that the shortest allowed output size for the SHAKE functions is actually 0 bits.

Table 4 in p. 23 of the document summarizes the security levels of the various SHA functions. For the SHAKEs, the security levels are given by formulas that take the output size d as a parameter. For example, for SHAKE128:

• Collision resistance is min(d/2, 128) bits;
• Preimage resistance is min(d, 128) bits.
• Second preimage resistance is also min(d, 128) bits.

Applying those formulas, when d = 0 we get these security levels (for both SHAKE128 and SHAKE256):

• 0 bits of collision resistance;
• 0 bits of preimage resistance;
• 0 bits of second preimage resistance.

A n-bit security level means that an attacker is guaranteed to succeed in no more than 2^n attempts. So a 0-bit security level means that an attacker succeeds in no more than 2^0 attempts. And as proof of that, here's a successful collision attack on 0-bit output length SHAKE256:

SHAKE256(0x00, 0) = SHAKE256(0xff, 0)

So the math works out just fine, and zero-length SHAKE outputs are exactly as secure as they sound.

---

Knowing that longer output is obviously better (higher entropy) [...]

As other answers have pointed out, longer doesn't necessarily mean better. The formulas I referred to above (p. 23 of FIPS 202) give a precise answer:

• The security levels of SHAKE128 and SHAKE256 as hash functions cannot exceed 128- and 256-bits respectively;
• If your output is short enough the security level will be below those values.

Answer 4

The Keccak function has an internal state of 1600 bit, at one point it was as high as 4800 bit... regardless of output size the Internal state is what determines security, not the length that it is compressed to.