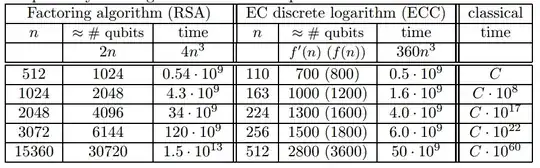
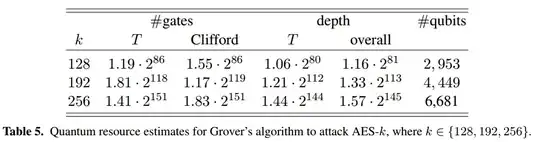
Assuming quantum computing continues to improve and continues to perform like this:
... quantum computer completes 2.5-billion-year task in minutes
is it reasonable to expect that 256 bit encryption will be possible to brute force at some point in the future, and if so, what estimates (preferably from large tech companies, security companies, academics, or government organisations) are available as to when that may start to occur?
Notes
Obviously estimates would be extremely difficult to make, and probably depend heavily on a few key assumptions (and even then it could happen much earlier or much later than predicted), but despite the difficulty of such predictions, some rules of thumb (e.g. Moore's Law) have performed reasonably well given the difficulty of such predictions.
Since the US Government considers 256 bit encryption safe enough to not be broken (by any one outside the US) for a time scale long enough to protect US security interests (last paragraph), we can assume it's a fairly long way away.
Background: