4

I'm trying to understand the dynamics of the authentication process in the MS-CHAPV2 protocol. In particular, if I implement an Evil Twin attack I can't understand how it's possible that I can retrieve the NTLM v1 password. From the implementation of the MS-CHAPV2, it seems it is not possible.

This is the context: A hacker sets his notebook to perform an Evil Twin attack on a WPA2-Enterprise network. He will impersonate the correct Access Point and the correct Authentication Server, waiting for some clients to connect to his notebook in order to steal their credentials and to impersonate them in the enterprise network.

The network uses MS-CHAPV2 as the inner authentication protocol.

When the client starts the EAPOL process to access to this fake network, we arrive at the inner authentication process (of the client at the server):

enter image description here

This process follows these steps:

  1. The client starts the protocol with a “hello" message.
  2. The authentication server answers with a 16 Byte ServerChallenge.
  3. The client combines the ServerChallenge, a 16 Byte random ClientChallenge, and the username to create the ChallengeHash.
  4. The client then calculates the NTHash which is the MD4 hash of the user’s password and pads this with zeros to 21 bytes.
  5. Client splits the 21 Byte long NTHash in three 7 Byte long DES keys. A parity bit is added to each 7 bits to create a 8 Byte long DES key.
  6. Each key is used to encrypt the ChallengeHash. The concatenation of these three ChallengeHashes forms the ChallengeResponse.
  7. The 24 Byte ChallengeResponse, 16 Byte ChallengeHash and the UserName is sent to the AS.
  8. The AS has to answer with an AuthenticationResponse which uses the md4 hash of the md4 hash of the user’s password combined with the ChallengeResponse sent by the user, two constant sentences and the ChallengeHash. This message is sent to verify that the server knows the password as well.

As an attacker, I can see all the information received by the client and all the information sent by the server. However, if the client uses the "MD4(UserPassword)" string as a key to encrypt the 3 different parts of the challenge response (see point 5), how can it be possible that I can obtain this MD4 password?

Why could I obtain, in my testing process, something like this (NTLMV1 hash)? (I'm using hostapd-wpe)

enter image description here

usern3t
  • 41
  • 1
  • 3

1 Answers1

2

TL;DR - You can trivially brute-force the DES keys used in the challenge/response mechanism. In order to reverse the challenge/response mechanism you only have to brute-force two DES iterations that have a 56-bit key.

In order to obtain the NT hash, you will need to concatenate the challenge & the first two-thirds of your response and K3 as Base64.

NTLM is a challenge-response authentication protocol essentially what this means is, one party will present a challenge and the other party must provide a valid response - if this doesn't happen then authentication will not take place.

A good way of picturing this would be a security question - imagine if to unlock your account you had to provide the correct answer to the following security question; What was the name of your childhood pet? While this is not exactly what this would look like it's a nice way of picturing it.

High-Level Overview

NTLM has three messages to authenticate a client, these messages are defined in the following Microsoft document NTLM Messages

  • NEGOTIATE_MESSAGE
  • CHALLENGE_MESSAGE
  • AUTHENTICATE_MESSAGE

These messages are sent in the order they are listed in, we will change the notation of these messages to be NM, CM and AM.

Firstly the client will send the NM to the server this will allow the client to inform the server what NTLM options it supports, upon negotiating this the server will then send a CM to the client. The idea behind the CM is so that the client can prove it's identity to the server. Finally, the client will send an AM back to the server after the CM has been processed by the client.

Hashing

NTLM uses two hashed passwords which are stored on the server and while they are salted before they are sent over the wire they are not salted in the machine's memory, this is an issue because if you obtain the hash value from the server you can use it to authenticate without even needing the password.

The first hash is known as the LM and the other is known as the NT. The LM uses a DES-Based function and the NT uses MD4.

LM

The linked diagram shows how the LM hash is calculated using the example of "napier" alternatively the below steps follows the same premise.

  1. Convert user's password to uppercase, then pad the provided password up to 14 bytes using NULL-padding
  2. Split the 14 byte password into two 7-byte halves
  3. Create two 64-bit DES keys using the 7-byte halves (with the addition of a parity bit for every seven bits)
  4. Each key is used to encrypt the string KGS!+#$% which returns two 8-byte cipher values.
  5. The resulting two values are concatenated to give a 16-byte hash.

It is not certain why "KGS!+#$%" is chosen however as per the below on the LAN Manager Wikipedia page it would seem the reason is related to the writers of RFC 2443.

The string “KGS!+#$%” could possibly mean Key of Glen and Steve and then the combination of Shift + 12345. Glen Zorn and Steve Cobb are the authors of RFC 2433 (Microsoft PPP CHAP Extensions). - LAN Manager Note 2.

NT

With the NT hash each character is converted into UTF-16 and uses a Little Endian format, I am not going to go into detail about Endianness here so, unfortunately, it will require research if you're unsure of what that means.

Lets look at another diagram using the "napier" example again in the following diagram you can see we take the word napier and after every character we have a null-byte for example "napier" becomes 'n' 0 'a' 0 'p' 0 'i' 0 'e' 0 'r' 0 as shown in the linked diagram, this is the result of encoding "napier" with UTF-16-LE. Then we use an MD4 signature taken from the string which returns a 128-bit code that in our example would be 307E40814E7D4E103F6A69B04EA78F3D you can try this out yourself using this MD2/MD4 encryption site. In essence, the function would look like this to get the NT hash: MD4(UTF-16-LE(password))

Low-Level Overview

Now that we have discussed the hashing and a high-level overview of the challenge/response authentication method we will look at the low-level overview of how this works.

Both of the hashes above produce a 16-byte value, 5-bytes of 0s are appended to reach 21-bytes. Those 21 bytes are separated into three 7-byte values. Each 7-byte value is used as a key to DES encrypt the 8-byte challenge we send to the client. The three encryptions are then used to form the 24-byte response.

  1. The server will authenticate by sending an 8-byte random number known as the challenge. (See above)
  2. The client will perform an operation involving the challenge and a secret which is shared between the client and the server, this secret will be one of the two password hashes we described previously.
  3. The client then returns a 24-byte result from the computation. It's typical in NTLMV1 that both hashes will be used for the computation and thus both 24-byte results are sent back.
  4. The server will then verify that the client has computed the correct result, if they have the server will infer possession of the secret and hence the client's authenticity.

In essence, the below code-block shows how the steps performed look with the mathematical notation.

C = 8-byte server challenge, random
K1 | K2 | K3 = NTLM-Hash | 5-bytes-0
Response = DES(K1,C) | DES(K2,C) | DES(K3,C)

Hashing/Encryption weaknesses

NTLM is a very old protocol - usually, older protocols don't survive (if there are issues with them). NTLM is one of those older protocols that didn't survive the test of time. Firstly the functions that are used are too weak/cheap for modern day hardware.

Let's look at DES, DES was first published in 1975, it's a very old protocol, one of the main issues with DES is how weak it is against brute-force attacks, especially in the modern age. In fact as per DES Strengths and Weaknesses it would seem that even in 1977 with enough money it would be possible to brute-force DES.

In 1977, Diffie and Hellman proposed a machine costing an estimated US$20 million which could find a DES key in a single day.

So it is arguable that DES was never strong against brute force attacks (the standardized post-NSA consultation version anyways - originally the designers did propose a "real" key size).

If you're wondering about the maths behind how long it would take to find a DES key compared to an AES key see: How long does it take to crack DES and AES?, the top answer clearly presents the length of time it would take, just be aware post is from '11, things do change and so does computing power so that is something to factor in, see that answer as a guideline rather than an exact figure.

In essence, the time it would take to brute-force a DES key (especially with today's computing) is way too short for it to be considered up to the modern standards and thus it's become obsolete.

What about MD4? Let's take a look at Message Digest 4. As you may be aware we now have MD5 which like MD4 is still pretty weak for things such as password-hashing due to its speed.

Whilst MD4 is a relatively "new" hashing function, it is still weak. It was first published in 1990 by Ronald Rivest who is incredibly well-versed in Cryptography and well-known to Cryptographers.

MD4's problem (and MD5's in-fact) is how cheap it is to compute collisions; in short, a collision is where a function maps two distinct inputs to the same output, a collision-attack describes the process of attempting to find two inputs that produce the same output. Computing collisions in MD4 is really fast & incredibly cheap. In-fact there was a collision attack published in 2007 that could find a collision in less than two hash operations.

Other Weaknesses

One distinct issue is the ability to perform a relay attack fairly trivially see: Practical guide to NTLM Relaying

I won't go into it here for the sake of post length however the above linked should have more than sufficient detail.

Weaknesses in MSCHAPV2

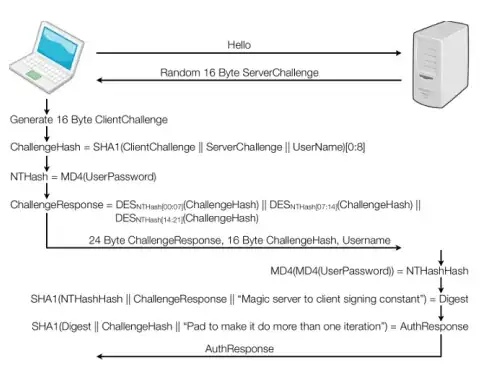
As for weaknesses in MS-CHAPV2, in step four of the process because the NT hash is not salted as an attacker you can reuse it, this means the NTHash is used as the password, meaning that we can use it to authenticate as the user; to add to that we can also impersonate the AS and authenticate the user. Because there is no salt being used this allows us to use rainbow tables.

Another blatant issue is in step six where you can easily perform a brute-force attack on each key fairly trivially see: Evil Twin Vulnerabilities in Wi-Fi Networks

Further Reading

MD4

DES Challenges

DES

NT & LM Hash

Stop using NTLMV1

LM, NTLM, Net-NTLMv2, oh my!

Community
  • 1