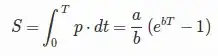First I apologize that I don't have a real answer to your question, but my hunch is yes. And I've been working to derive a similar formula from a fairly specific scenario, but I believe if I can prove my hypothesis, it could be generalized more to actually answer your question fully.
I've received similar resistance from folks concerned with the "practical significance" of results from a strict and unrealistic hypothetical scenario. The concerns of infinite resources is valid, but Rock's law can indeed be factored in mathematically for a more accurate analysis of the problem. Still, I think it's unsafe from a defender's perspective to place strict limits on the resources available to any the attacker of actual concern in the first place for a number of practical reasons to include the realistic assumption that by her very nature, an attacker may at any point in time have access to any number of stolen credit cards, for example.
I used the what I was taught to be a more accurate assumption that processing power doubles every 18 months.
In other words, if at time 0 processing power is P(O), in 18 months, the processing power available is P(0)*2^1.5. (It is worth noting that after 3 years, the processing power has therefore exactly quadrupled).
I'm still struggling to prove the observations I made with a spreadsheet mathematically but I'm pretty confident in my formulas. I found the almost too obvious to trust results that no mater what the initial processing speed is, and regardless of how many years it takes to get to this point, after you have cracked 1/4 of the total password space, you will crack the remaining 3/4 in no more than three years! Since processing power quadruples in 3 years, this seems plausible, but the natural doubt is in determining the initial processing power as it seems that would significantly impact the observations.
I've tried playing with keyspace and initial inputs, but haven't been able to break my spreadsheet yet.
I computed that on an annual basis, the processing power increases by 2^(2/3) to develop a discrete recurrence relationship.
Scenario wise, this means that the attacker upgrades annually to the current processing power without loss of time. Yes it's unrealistic from an absolute perspective, but I'm working under the assumption that the relative significance of transfer time will trend toward 0 as processing power and key space increases. And would bet dollars to donuts this could be proven mathematically.
So the relationship becomes
Given some constant P(0), P(1) = P(0)*2^(2/3). P(2) = P(1) * 2^(2/3) = P(0) * 2^(2/3) * 2^(2/3).
We can see soon that P(i) = P(0) * 2^(2i/3).
So we have defined P(i) as the number of password cracked in year i using the processing power available at the beginning of year i.
In other words, P(n) = P(0)*2((2*0)/3) + P(0)*2((2*1)/3) + P(0)*2((2*2)/3) + ... P(0)2((2(n-1))/3) + P(0)*2((2*n)/3).
Or P(0)(1 + 2^(2/3) + 2^(4/3) + ... + 2^((n-1)/3) + 2^(2n/3))
Now we can look at the relationship between password space and time taken to crack additional space.
We were given that a 128 bit keyspace can be cracked in 100 years, and determined that adding two more bits (for a total of 130 bits) quadrupled the key space.
So regardless of the original process speed or keys cracked in one year, we know that after 100 years we have cracked the full 128 bit space and that that space is 1/4 of the new password space. So after 100 years we have cracked 1/4 of the total space, and we want to know how many more years before we crack the remaining 3/4.
Lets start at n years to crack the full space which we can express as:
P(n) = P(0)(1 + 2^(2/3) + 2^(4/3) + ... + 2^((n-1)/3) + 2^(2n/3)) = 100% of the space.
And the year before (n-1) we have cracked a total of
P(n-1) = P(0)(1 + 2^(2/3) + 2^(4/3) + ... + 2^((n-1)/3))
What fraction of the total key space have we cracked by year n-1?
P(0)(1 + 2^(2/3) + 2^(4/3) + ... + 2^((n-1)/3))
P(0)(1 + 2^(2/3) + 2^(4/3) + ... + 2^((n-1)/3) + 2^(2n/3))
And
P(n-3)
P(n)
=
P(0)(1 + 2^(2/3) + 2^(4/3) + ... + 2^((n-3)/3))
P(0)(1 + 2^(2/3) + 2^(4/3) + ... + 2^((n-1)/3) + 2^(2n/3))
And here's where my arithmetic and induction and mathematical foundations continues to fail me, and I get stymied with a formal proof, but my observations suggest this should simplify to 1/4 for significantly sized n.
My interest is in determining a mathematical proof to explain the somewhat intuitive but nonetheless surprising conclusions.
Mine is a question to help determine the maximum additional security a fixed expansion of password space actually adds in terms of the time it takes for a cracker to fully compute all possible pawned hashes in a given space.
We have to accept a lot of less-than realistic assumptions for the different variables to develop a strict mathematically provable relationship from which to then determine if our assumptions about the added benefit of additional characters in a password length are realistic to begin with.
I was given a test problem: if a cracker can compute the every hash in a key space defined from a 128 character binary alphabet, how long will it take her to crack a 130 bit binary key space?
The "correct" answer was 400 years. I argued that the question was poorly defined since taking Moore's law into account we know that even though the key space has quadrupled (2 additional bits creates 4 times as many options assuming all options are valid passwords) the time taken to crack it will be less than four times as long.
"Significantly" less is indeed accurate, but after failing to define how much less through a formal proof, I used a spreadsheet to generate hard data to help guide my approach to the proof.