Truth table
A truth table is a table that lists all possible states of a statement.[1] Truth tables are commonly used to compare statements; if two statements share the same truth table, then the two statements are said to be logically equivalent. Truth tables are also able to be used to find negations of statements.
| Cogito ergo sum Logic and rhetoric |
 |
| Key articles |
| General logic |
| Bad logic |
|
v - t - e |
Equivalent statements
If two statements,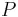 
and 
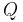, have truth tables that contain the same elements, then the two statements are logically equivalent.[2][3] That is, the two statements will be true or false under the same conditions. 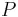and 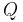being logically equivalent is denoted as: 
. Finding equivalent statements is a tool used in mathematics as it may be difficult to directly prove one statement, but easy to prove an equivalent statement.
Example of equivalent statements
One can show that, for two statements 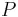and ,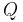 
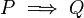is logically equivalent to 
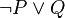by showing that they have the same truth table. Consider the truth table for :
| | |
|---|---|---|
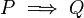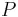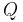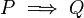| T | T | T |
| F | F | T |
| T | F | F |
| F | T | T |
In the above table, T is true and F is false. Now consider the truth table for :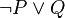
| | |
|---|---|---|
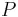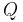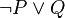| T | T | T |
| F | F | T |
| T | F | F |
| F | T | T |
Observing the two tables, they have the same elements. Thus, 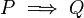is logically equivalent to .
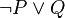Negation of statements
Given a statement 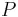, another statement 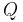is the negation of 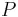if the state of 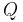is opposite of 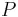given the same conditions. That is, 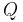is false when 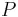is true, and 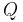is true when 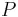is false. If this holds, then 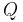is the negation of 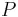, written as 
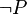(sometimes as ~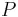).[4]
| |
|---|---|
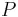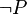| T | F |
| F | T |
The negation of 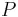, , 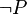is visualized in the above truth table.
Example of negated statements
One can show that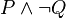 
is the negation of 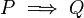via a truth table.
| | | |
|---|---|---|---|
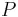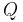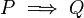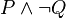| T | T | T | F |
| F | F | T | F |
| T | F | F | T |
| F | T | T | F |