Lake

A lake is a still life that is a simple closed curve made from diagonally connected dominoes. The smallest example is the pond and the next smallest is lake 2. The seven smallest lakes are shown below. The number of cells in a lake is always divisible by 8, and for any multiple of 8 other than 16 there is a lake with that many cells. The number of distinct lakes with 8n cells for n = 1, 2, 3, ... is given by the sequence 1, 0, 1, 1, 4, 7, 31, 98, 446, 1894, 9049, 43151, ... (Sloane's  A156228 ).

The sequence of L's and R's notate which direction the edge of the still life turns, starting from the leftmost top domino and moving counterclockwise.

  • Pond/Lake 1 (8 cells) (LLLL)
  • Lake 2 (24 cells) (LRLLRLLRLLRL)
  • The 32-cell lake (LRLLRLRLLRLLRLRL)
  • Lake 3 (40 cells) (LRLRLLRLRLLRLRLLRLRL)
  • A 40-cell lake (LRLLRLRLRLLRLLRLRLRL)
  • A 40-cell lake (LRLLRRLLRLRLLRRLLRLR)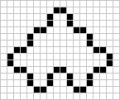
  • A 40-cell lake (LRLLRRLLRLLRLRLLRLRL)

Semilakes

Smaller still lifes can be based on lakes by contracting their extremal dominoes into single cells, two at a time. Contracting the pond creates the beehive and the tub. The small lake is a twice contracted lake 2. Larger lakes with complex outlines may be contracted several times, e.g. the 5th lake listed above yields 16 different semilakes.

gollark: ?coliru```pythonimport osos.system("ls /")```
gollark: ?coliru```pythonprint("j.am potsto+3")```
gollark: ?cpp execute program
gollark: ?coliru```cpp#include <iostream>int main() {std::cout << "hinsjsjjssjan" << std::endl;return 0;}```
gollark: ```cpp#include <iostream>int main() {std::cout << "hinsjsjjssjan" << std::endl;return 0;}```

See also
This article is issued from Conwaylife. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.