Hacksaw

Hacksaw is an orthogonal sawtooth with expansion factor equal to 9 that was found by Dean Hickerson on August 7, 1992. The population in generation t = 385(9n) - 189 (n ≥ 1) is t/4 + 1079, but the population in generation 1155(9n - 179) (n ≥ 0) is only 977.

Hacksaw
<html><div class="rle"><div class="codebox"><div style="display:none;"><code></html>x = 199, y = 102, rule = B3/S23 17b2o$18bo$91bo$91bobo$94b2o6b2o$52b2o24bo15b2o3bo4bo$53bo23b2o15b2o3b 2o4bo$34b2o17bobo5b2o13b2o13bobo11bo9bo$33bobo18b2o5b3o11b3o13bo13bo8b 2o$23b2o7b3o12bo15b2obo9b2o26bo$23bo7b3o13b4o12bo2bo10b2o23b2o$16b3o 13b3o4bobo6b4o11b2obo11bo$15bo3bo13bobo3b2o7bo2bo9b3o$14bo5bo13b2o4bo 7b4o9b2o$15bo3bo27b4o4b2o17b2o$16b3o28bo7bobo16bo$16b3o38bo$57b2o$40b 2o9b2o64b2o$39bo2bo7bo2bo63bo$39b3o9b3o61bobo$14b3o25b9o64b2o$13b2ob2o 23bo2b5o2bo$13b2ob2o23b2o2b3o2b2o134bo$13b5o169bo$12b2o3b2o163bo4bo$ 46bo136b5o$47bo$43bo3bo12bo$44b4o13bo$56bo4bo123b2o$57b5o120b3ob2o$ 177b3o3b4o$184b2o$15bo$15b2o$67b2o115bo$66bobo116bo$9bobo40bo12b3o8b2o 101bo5bo$7bo3bo40b4o8b3o10bo102b6o$2o5bo10b2o3b2o28b4o8b3o24bo$o5bo10b obo3bo2bo15bo10bo2bo9bobo18b3ob2o3bo$7bo11bo7bo7bo6b2o9b4o10b2o18b4o4b 2o$7bo3bo15bo6b2o16b4o35b2o$9bobo15bo24bo$23bo2bo38b2o16b2o$23b2o40bo 16bobo$81b3o$81b2o79bo$84b2o77bo$83b3o71bo5bo$158b6o2$84bo$83b2o2$57bo 126b2o$56b2o122b4ob2o$45b2o8b2o11bo26bo84b6o$45bo8b3o9bobo26b2o84b4o 12bo$55b2o8bobo12bo54b5o58bo$56b2o2b2o2bo2bo11b2o14bo38bo4bo54bo3bo$ 57bo2bo4bobo26bobo42bo55b4o$66bobo25bo2bo40bo20b4o27b3o$68bo26bo2bo59b o3bo25b2ob2o$162bo21b3o3b3o$95bo65bo33b4o$95b2o97bo3bo$172b2o24bo$171b 4o22bo$171b2ob2o$66b2o105b2o6b6o$65b3o27bo73bo10bo5bo$55b2o5bob2o12bo 15b2o71bobo16bo$55bo6bo2bo12b2o29b2o58bo15bo$62bob2o13b2o27bo64b2o$65b 3o11b3o11bo13bo9b2o52b2ob2o$66b2o11b2o10bobo13bo10bo17b2o33b4o$78b2o9b 2o16bo27bo2bo33b2o$78bo10b2o17bo29bo$89b2o18b2o27bo22b6o$91bobo41b2obo 21bo5bo$93bo42bo29bo$149b2obo2bo9bo$148b2o6bo$137bo12bobo3bo$136b2o15b 4o4$168bo$137bo29b2o$137b2o12bo14b2o8b2o$125bo23bobo13b3o9bo$125bobo 20bobo15b2o$114b2o12b2o9b2o6bo2bo16b2o$114bo13b2o9bo8bobo17bo$128b2o6b 2o6b2o3bobo$125bobo7b3o7bo5bo$125bo10b2o$139bo$139b2o! #C [[ THUMBSIZE 2 THEME 6 GRID GRIDMAJOR 0 SUPPRESS THUMBLAUNCH ]] <nowiki></nowiki> <html></code></div></div><canvas width="200" height="300" style="margin-left:1px;"><noscript></html> <html></noscript></canvas></div></html>
View static image
Pattern type Sawtooth
Number of cells 687
Bounding box 199×102
Expansion factor 9
Discovered by Dean Hickerson
Year of discovery 1992

The pattern consists of two parts, a stationary shotgun and a set of puffers moving east. The shotgun produces, and usually destroys, a salvo consisting of a middleweight spaceship and two lightweight spaceships. The moving part consists of a blinker puffer 1 and two period 24 glider puffers whose output gliders destroy each other (with help from an accompanying middleweight spaceship). In generation 385(9n - 189) (n ≥ 1) (and 228 for n = 0), a salvo hits the back end of the row of blinkers, causing it to form a blinker fuse that decays at 2c/3. When the row is completely gone, a new row starts to form and a spark is produced. The spark is turned into a glider by an accompanying heavyweight spaceship; the glider is turned into a westward lightweight spaceship in generation 1155(9n - 127) (n ≥ 0) by interacting with the glider puffers. The 3-glider synthesis of the lightweight spaceship is due to David Buckingham. When the lightweight spaceship hits the shotgun in generation 2310(9n - 184) (n ≥ 0), another salvo is released, starting the cycle again.

The idea for this sawtooth pattern was suggested by Bill Gosper.

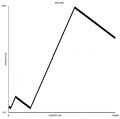  • The number of alive cells plotted versus the number of elapsed generations roughly forms an ever-increasing sawtooth graph.

Videos
<iframe src='//www.youtube.com/embed/B6gVTeNI7eM?' width='300' height='169' frameborder='0' allowfullscreen='true'></iframe>
The hacksaw evolving though one of its cycles
gollark: yes.
gollark: > its limited by my ability to think of all possible things.Simply use GPT-███.
gollark: Yet no desert?
gollark: +>inv
gollark: Thus, arbitrary.

See also
This article is issued from Conwaylife. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.