21
Continued fractions are expressions that describe fractions iteratively. They can be represented graphically:
Or they can be represented as a list of values: [a0; a1, a2, a3, ... an]
The challenge:
take a base number: a0 and a list of denominator values: [a1, a2, a3, ... an] and simplify the continued fraction to a simplified rational fraction: return or print numerator and denominator separately.
Examples:
√19 : [4;2,1,3,1,2]: 170/39ℯ: [1;0,1,1,2,1,1]: 19/7π: [3;7,15,1,292,1]: 104348/33215ϕ: [1;1,1,1,1,1]: 13/8
Example implementation: (python)
def foo(base, sequence):
numerator = 1
denominator = sequence[-1]
for d in sequence[-2::-1]:
temp = denominator
denominator = d * denominator + numerator
numerator = temp
return numerator + base * denominator, denominator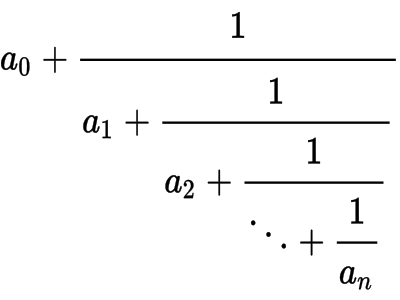
You should make this sentence more clear, "and simplify the continued fraction to a single fraction"; unless you intended the wording to mean a result of
2.002can be expressed as2002/1000. That's technically a "single fraction", you probably want to say, "a single fraction, in its most simple form." – Magic Octopus Urn – 2016-09-14T20:29:45.673@carusocomputing point taken.. although I wouldn't feel too bad about 2/4 (or similar) as it has still simplified the multiple fraction structure to a single fraction – Aaron – 2016-09-14T20:47:09.113
Hmm... I think there's a way to exploit that, but with the 13 byte golfscript answer, I'd have to probably use MATL to win. – Magic Octopus Urn – 2016-09-14T21:00:46.803
@carusocomputing I'd say go for it... If you can beat the 13 byte answer, that'd be awesome – Aaron – 2016-09-14T21:29:33.693
You can make the pi stop earlier - 355/113. – Thorbjørn Ravn Andersen – 2016-09-14T21:54:08.247
@ThorbjørnRavnAndersen all of them can in fact stop whenever, or never at all, as they're all infinite series expansions... – Aaron – 2016-09-15T13:04:47.753
Related challenge, and Another – mbomb007 – 2016-09-16T18:12:59.130
@mbomb007 those two are exactly the same as each other, whereas mine reverses the inputs and outputs of the question... Obvi they're related, but the exact question hadn't been asked yet – Aaron – 2016-09-20T23:19:52.553