Determining the continued fractions of square roots

Question

The continued fraction of a number n is a fraction of the following form:


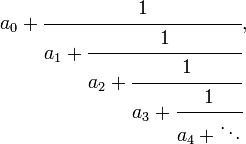
which converges to n.

The sequence a in a continued fraction is typically written as: [a₀; a₁, a₂, a₃, ... a_n].
We will write ours in the same fashion, but with the repeating part between semicolons.

Your goal is to return the continued fraction of the square root of n.
Input: An integer, n. n will never be a perfect square.
Output: The continued fraction of sqrt(n).

Test Cases:
2 -> [1; 2;]
3 -> [1; 1, 2;]
19 -> [4; 2, 1, 3, 1, 2, 8;]

Shortest code wins. Good luck!

Answer 1

GolfScript (66 60 chars)

~:^,{.*^>}?(:?';'[1?{^1$.*-@/?@+.2$/@@1$%?\- 1$(}do;;]','*1$

Warning: most of the ? in there are the variable representing floor(sqrt(input)) rather than the builtin. But the first one is the builtin.

Takes input on stdin and outputs to stdout.

Psuedocode of the algorithm (proof of correctness currently left as an exercise for the reader):

n := input()
m := floor(sqrt(n))
output(m)
x := 1
y := m
do
  x := (n - y * y) / x
  output((m + y) / x)
  y := m - (m + y) % x
while (x > 1)

Yet again I find myself wanting a single operator which takes a b on the stack and leaves a/b a%b on the stack.

Answer 2

Python, 95 97 (but correct...)

This uses only integer arithmetic and floor division. This will produce correct results for all positive integer inputs, though if one wants to use a long, they'd have to add a character; for example m=a=0L. And of course... wait for a million years for my poor man's floor sqrt to terminate.

z=x=m=1
while n>m*m:m+=1
m=y=m-1
l=()
while-z<x:x=(n-y*y)/x;y+=m;l+=y/x,;y=m-y%x;z=-1
print c,l

Output:

n=139
11 (1, 3, 1, 3, 7, 1, 1, 2, 11, 2, 1, 1, 7, 3, 1, 3, 1, 22)

edit: now using Peter Taylor's algorithm. That do...while was fun.

Answer 3

Python, 87 82 80

x=r=input()**.5
while x<=r:print"%d"%x+",;"[x==r],;x=1/(x%1)
print`int(r)*2`+";"

It takes one integer and gives output like:

4; 2, 1, 3, 1, 2, 8;

Answer 4

Mathematica 33 31

c[n_]:=ContinuedFraction@Sqrt@n

Output is in list format, which is more appropriate for Mathematica. Examples:

c[2]
c[3]
c[19]
c[139]
c[1999]

(* out *)
{1, {2}}
{1, {1, 2}}
{4, {2, 1, 3, 1, 2, 8}}
{11, {1, 3, 1, 3, 7, 1, 1, 2, 11, 2, 1, 1, 7, 3, 1, 3, 1, 22}}
{44, {1, 2, 2, 4, 1, 1, 5, 1, 5, 8, 1, 3, 2, 1, 2, 1, 1, 1, 1, 1, 1, 
  1, 14, 3, 1, 1, 29, 4, 4, 2, 5, 1, 1, 17, 2, 1, 12, 9, 1, 5, 1, 43, 
  1, 5, 1, 9, 12, 1, 2, 17, 1, 1, 5, 2, 4, 4, 29, 1, 1, 3, 14, 1, 1, 
  1, 1, 1, 1, 1, 2, 1, 2, 3, 1, 8, 5, 1, 5, 1, 1, 4, 2, 2, 1, 88}}

Answer 5

APL(NARS), 111 chars, 222 bytes

r←f w;A;a;P;Q;m
m←⎕ct⋄Q←1⋄⎕ct←P←0⋄r←,a←A←⌊√w⋄→Z×⍳w=0
L: →Z×⍳0=Q←Q÷⍨w-P×P←P-⍨a×Q⋄r←r,a←⌊Q÷⍨A+P⋄→L×⍳Q>1
Z: ⎕ct←m

The f function is based on the algo one find in the page http://mathworld.wolfram.com/PellEquation.html for solve Pell equation. That f function has its input all not negative number (type fraction too). Possible there is something goes wrong, I remember that √ has, in how I see it, problem for big fraction numbers, as

  √13999999999999999999999999999999999999999999999x
1.183215957E23 

so there would be one function sqrti(). For this reason fraction input (and integer input) has to be <10^15. test:

 ⎕fmt (0..8),¨⊂¨f¨0..8
┌9───────────────────────────────────────────────────────────────────────────────────────────────────────┐
│┌2─────┐ ┌2─────┐ ┌2───────┐ ┌2─────────┐ ┌2─────┐ ┌2───────┐ ┌2─────────┐ ┌2─────────────┐ ┌2─────────┐│
││  ┌1─┐│ │  ┌1─┐│ │  ┌2───┐│ │  ┌3─────┐│ │  ┌1─┐│ │  ┌2───┐│ │  ┌3─────┐│ │  ┌5─────────┐│ │  ┌3─────┐││
││0 │ 0││ │1 │ 1││ │2 │ 1 2││ │3 │ 1 1 2││ │4 │ 2││ │5 │ 2 4││ │6 │ 2 2 4││ │7 │ 2 1 1 1 4││ │8 │ 2 1 4│││
││~ └~─┘2 │~ └~─┘2 │~ └~───┘2 │~ └~─────┘2 │~ └~─┘2 │~ └~───┘2 │~ └~─────┘2 │~ └~─────────┘2 │~ └~─────┘2│
│└∊─────┘ └∊─────┘ └∊───────┘ └∊─────────┘ └∊─────┘ └∊───────┘ └∊─────────┘ └∊─────────────┘ └∊─────────┘3
└∊───────────────────────────────────────────────────────────────────────────────────────────────────────┘
  f 19
4 2 1 3 1 2 8 
  f 54321x
233 14 1 1 3 2 1 2 1 1 1 1 3 4 6 6 1 1 2 7 1 13 4 11 8 11 4 13 1 7 2 1 1 6 6 4 3 1 1 1 1 2 1 2 3 1 1 14 466 
  f 139
11 1 3 1 3 7 1 1 2 11 2 1 1 7 3 1 3 1 22 
  +∘÷/f 139
11.78982612
  √139
11.78982612

if the argument is a square of a number it would return one list of 1 only element, the sqrt of that number

  f 4
2 

If it would depend from me, in one exercise without "codegolf" I would prefer the previous edit that use function sqrti()...

Answer 6

Python (136 133 96)

The standard method for continued fractions, extremely golfed.

a=input()**.5
D=c=int(a);b=[]
while c!=D*2:a=1/(a%1);c=int(a);b+=[c]
print D,";%s;"%str(b)[1:-1]

Answer 7

Perl, 99 chars

Does not screw up on 139, 151, etc. Tested with number ranging from 1 to 9 digits.

$"=",";$%=1;$==$-=($n=<>)**.5;
push@f,$==(($s=$=*$%-$s)+$-)/($%=($n-$s*$s)/$%)until$=>$-;
say"$-;@f;"

Note: $%, $=, and $- are all integer-forcing variables.

Answer 8

C, 137

Including the newline, assuming I don't have to roll my own square root.

#include<math.h>
main(i,e){double d;scanf("%lf",&d);e=i=d=sqrt(d);while(i^e*2)printf("%d%c",i,e^i?44:59),i=d=1.0/(d-i);printf("%d;",i);}

It breaks for sqrt(139) and contains the occasional extra semicolon in the output, but I'm too tired to work on it further tonight :)

5
2;4;
19
4;2,1,3,1,2,8;
111
10;1,1,6,1,1,20;